mirror of
https://github.com/revarbat/BOSL2.git
synced 2025-08-18 18:51:30 +02:00
Merge remote-tracking branch 'upstream/master'
This commit is contained in:
189
attachments.scad
189
attachments.scad
@@ -1881,7 +1881,7 @@ module hide(tags)
|
||||
// attach(RIGHT,BOT) cyl(r=1,h=5);
|
||||
// attach(LEFT,BOT) cyl(r=1,h=5);
|
||||
// }
|
||||
// Example: Nexting applications of hide_this()
|
||||
// Example: Nesting applications of hide_this()
|
||||
// $fn=32;
|
||||
// hide_this() cuboid(10)
|
||||
// attach(TOP,BOT) cyl(r=2,h=5)
|
||||
@@ -3982,8 +3982,8 @@ function _find_anchor(anchor, geom)=
|
||||
pos2 = rot(from=UP, to=axis, p=pos),
|
||||
vec2 = anch==CENTER? UP : rot(from=UP, to=axis, p=vec),
|
||||
// Set spin for top/bottom to be clockwise
|
||||
spin = anch.z!=0 && (anch.x!=0 || anch.y!=0) ? _compute_spin(vec2,rot(from=UP,to=axis,p=point3d(tangent)*anch.z))
|
||||
: anch.z==0 && norm(anch)>0 ? _compute_spin(vec2, (vec2==DOWN || vec2==UP)?BACK:UP)
|
||||
spin = anch.z!=0 && (!approx(anch.x,0) || !approx(anch.y,0)) ? _compute_spin(vec2,rot(from=UP,to=axis,p=point3d(tangent)*anch.z))
|
||||
: anch.z==0 && norm(anch)>EPSILON ? _compute_spin(vec2, (approx(vec2,DOWN) || approx(vec2,UP))?BACK:UP)
|
||||
: oang
|
||||
) [anchor, pos2, vec2, spin]
|
||||
) : type == "point"? (
|
||||
@@ -4448,7 +4448,7 @@ module expose_anchors(opacity=0.2) {
|
||||
// See Also: generic_airplane(), anchor_arrow(), show_anchors(), expose_anchors(), frame_ref()
|
||||
// Usage:
|
||||
// show_transform_list(tlist, [s]);
|
||||
// show_transform_list(tlist) {CHILDREN};
|
||||
// show_transform_list(tlist) CHILDREN;
|
||||
// Description:
|
||||
// Given a list of transformation matrices, shows the position and orientation of each one.
|
||||
// A line is drawn from each transform position to the next one, and an orientation indicator is
|
||||
@@ -5012,6 +5012,7 @@ function _canonical_edge(edge) =
|
||||
flip * edge;
|
||||
|
||||
|
||||
|
||||
// Section: Attachable Descriptions for Operating on Attachables or Restoring a Previous State
|
||||
|
||||
// Function: parent()
|
||||
@@ -5064,7 +5065,7 @@ module restore(desc)
|
||||
multmatrix(T) children();
|
||||
}
|
||||
else{
|
||||
assert(!is_undef(desc) && is_list(desc) && len(desc)==2, "Invalid desc");
|
||||
check=assert(is_description(desc), "Invalid description");
|
||||
T = linear_solve($transform, desc[0]);
|
||||
$parent_geom = desc[1];
|
||||
multmatrix(T) children();
|
||||
@@ -5076,46 +5077,61 @@ module restore(desc)
|
||||
// Topics: Descriptions, Attachments
|
||||
// See Also: parent(), desc_dist()
|
||||
// Usage:
|
||||
// point = desc_point(desc,[anchor]);
|
||||
// point = desc_point(desc,[p],[anchor]);
|
||||
// Description:
|
||||
// Computes the coordinates of the specified anchor point in the given description relative to the current transformation state.
|
||||
// Computes the coordinates of the specified point or anchor point in the given description relative to the current transformation state.
|
||||
// Arguments:
|
||||
// desc = Description to use to get the point
|
||||
// anchor = Anchor point that you want to extract. Default: CENTER
|
||||
// p = Point or point list to transform. Default: CENTER (if anchor not given)
|
||||
// --
|
||||
// anchor = Anchor point (only one) that you want to extract. Default: CENTER
|
||||
// Example(3D): In this example we translate away from the parent object and then compute points on that object. Note that with OpenSCAD 2021.01 you must use union() or alternatively place the pt1 and pt2 assignments in a let() statement. This is not necessary in development versions.
|
||||
// cuboid(10) let(desc=parent())
|
||||
// right(12) up(27)
|
||||
// union(){
|
||||
// pt1 = desc_point(desc,TOP+BACK+LEFT);
|
||||
// pt2 = desc_point(desc,TOP+FWD+RIGHT);
|
||||
// pt1 = desc_point(desc,anchor=TOP+BACK+LEFT);
|
||||
// pt2 = desc_point(desc,anchor=TOP+FWD+RIGHT);
|
||||
// stroke([pt1,pt2,CENTER], closed=true, width=.5,color="red");
|
||||
// }
|
||||
// Example(3D): Here we compute the point on the parent so we can draw a line anchored on the child object that connects to a computed point on the parent
|
||||
// cuboid(10) let(desc=parent())
|
||||
// attach(FWD,BOT) cuboid([3,3,7])
|
||||
// attach(TOP+BACK+RIGHT, BOT)
|
||||
// stroke([[0,0,0], desc_point(desc,TOP+FWD+RIGHT)],width=.5,color="red");
|
||||
function desc_point(desc, anchor=CENTER) =
|
||||
is_undef(desc) ? linear_solve($transform, [0,0,0,1])
|
||||
: let(
|
||||
anch = _find_anchor(anchor, desc[1]),
|
||||
T = linear_solve($transform, desc[0])
|
||||
// stroke([[0,0,0], desc_point(desc,anchor=TOP+FWD+RIGHT)],width=.5,color="red");
|
||||
function desc_point(desc, p, anchor) =
|
||||
is_undef(desc) ?
|
||||
assert(is_undef(anchor), "Cannot give anchor withot desc")
|
||||
let(
|
||||
T = matrix_inverse($transform)
|
||||
)
|
||||
apply(T, anch[1]);
|
||||
apply(T, default(p,UP))
|
||||
: assert(is_description(desc), "Invalid description")
|
||||
assert(num_defined([anchor,p])<2, "Cannot give both anchor and p")
|
||||
let (
|
||||
T = linear_solve($transform, desc[0]),
|
||||
p = is_def(p) ? p
|
||||
: let(anch = _find_anchor(anchor, desc[1]))
|
||||
anch[1]
|
||||
)
|
||||
apply(T, p);
|
||||
|
||||
|
||||
// Function: desc_dir()
|
||||
// Synopsis: Computes the direction in the current context of a direction from an attachable description
|
||||
// Synopsis: Computes the direction in the current context of a direction or anchor in a description's context
|
||||
// Topics: Descriptions, Attachment
|
||||
// See Also: parent(), desc_point()
|
||||
// Usage:
|
||||
// dir = desc_dir([desc],[anchor]);
|
||||
// dir = desc_anchor(desc,[dir], [anchor]);
|
||||
// Description:
|
||||
// Computes the direction in the current context of an anchor direction from an attachable description. If you don't give a description
|
||||
// then the direction is computed relative to global world coordinates.
|
||||
// Computes the direction in the current context of a direction in the context of the description. You can specify
|
||||
// the direction by giving a direction vector, or you can give an anchor that will be interpreted from the description.
|
||||
// If you don't give a description then the direction is computed relative to global world coordinates; in this case you
|
||||
// cannot give an anchor as the direction.
|
||||
// Arguments:
|
||||
// desc = Description to use. Default: use the global world coordinate system
|
||||
// anchor = Anchor to get the direction from. Default: UP
|
||||
// dir = Direction or list of directions to use. Default: UP (if anchor is not given)
|
||||
// --
|
||||
// anchor = Anchor (only one) to get the direction from.
|
||||
// Example(3D): Here we don't give a description so the reference is to the global world coordinate system, and we don't give a direction, so the default of UP applies. This lets the cylinder be placed so it is horizontal in world coordinates.
|
||||
// prismoid(20,10,h=15)
|
||||
// attach(RIGHT,BOT) cuboid([4,4,15])
|
||||
@@ -5123,17 +5139,39 @@ function desc_point(desc, anchor=CENTER) =
|
||||
// Example(3D,VPR=[78.1,0,76.1]): Here we use the description of the prismoid, which lets us place the rod so that it is oriented in the direction of the prismoid's face.
|
||||
// prismoid(20,10,h=15) let(pris=parent())
|
||||
// attach(RIGHT,BOT) cuboid([4,4,15])
|
||||
// position(TOP) cyl(d=2,h=15,orient=desc_dir(pris,FWD),anchor=LEFT);
|
||||
function desc_dir(desc, anchor=UP) =
|
||||
// position(TOP) cyl(d=2,h=15,orient=desc_dir(pris,anchor=FWD),anchor=LEFT);
|
||||
function desc_dir(desc, dir, anchor) =
|
||||
is_undef(desc) ?
|
||||
assert(is_undef(anchor), "Cannot give anchor without desc")
|
||||
let(
|
||||
T = is_undef(desc) ? matrix_inverse($transform)
|
||||
: linear_solve($transform, desc[0]),
|
||||
dir = is_undef(desc) ? anchor
|
||||
: let(anch = _find_anchor(anchor, desc[1]))
|
||||
T = matrix_inverse($transform)
|
||||
)
|
||||
move(-apply(T,CENTER), apply(T, default(dir,UP)))
|
||||
:
|
||||
assert(is_description(desc), "Invalid description")
|
||||
assert(num_defined([dir,anchor])<2, "Cannot give both dir and anchor")
|
||||
let(
|
||||
T = linear_solve($transform, desc[0]),
|
||||
dir = is_def(dir) ? dir
|
||||
: let(
|
||||
anch = _find_anchor(anchor, desc[1])
|
||||
)
|
||||
anch[2]
|
||||
)
|
||||
apply(T, dir)-apply(T,CENTER);
|
||||
move(-apply(T,CENTER),apply(T, dir));
|
||||
|
||||
function desc_attach(desc, anchor=UP, p, reverse=false) =
|
||||
assert(is_description(desc), "Invalid description")
|
||||
let(
|
||||
T = linear_solve($transform, desc[0]),
|
||||
anch = _find_anchor(anchor,desc[1]),
|
||||
centerpoint = apply(T,CENTER),
|
||||
pos = apply(T, anch[1]),
|
||||
y = apply(T*rot(from=UP,to=anch[2])*zrot(anch[3]),BACK)-centerpoint,
|
||||
z = apply(T,anch[2])-centerpoint
|
||||
)
|
||||
reverse ? frame_map(z=z,y=y,reverse=true, p=move(-pos,p))
|
||||
: move(pos,frame_map(z=z,y=y, p=p));
|
||||
|
||||
|
||||
// Function: desc_dist()
|
||||
@@ -5146,12 +5184,19 @@ function desc_dir(desc, anchor=UP) =
|
||||
// Description:
|
||||
// Computes the distance between two points specified using attachable descriptions and optional anchor
|
||||
// points. If you omit the anchor point(s) then the computation uses the CENTER anchor.
|
||||
// Arguments:
|
||||
// desc1 = First description
|
||||
// anchor1 = Anchor for first description
|
||||
// desc2 = Second description
|
||||
// anchor2 = Anchor for second description
|
||||
// Example(3D): Computes the distance between a point on each cube.
|
||||
// cuboid(10) let(desc=parent())
|
||||
// right(15) cuboid(10)
|
||||
// echo(desc_dist(parent(),TOP+RIGHT+BACK, desc, TOP+LEFT+FWD));
|
||||
|
||||
function desc_dist(desc1,anchor1=CENTER, desc2, anchor2=CENTER)=
|
||||
assert(is_description(desc1),"Invalid description: desc1")
|
||||
assert(is_description(desc2),"Invalid description: desc2")
|
||||
let(
|
||||
anch1 = _find_anchor(anchor1, desc1[1]),
|
||||
anch2 = _find_anchor(anchor2, desc2[1]),
|
||||
@@ -5163,13 +5208,12 @@ function desc_dist(desc1,anchor1=CENTER, desc2, anchor2=CENTER)=
|
||||
)
|
||||
norm(pt1-pt2);
|
||||
|
||||
|
||||
// Function: trans_desc()
|
||||
// Function: transform_desc()
|
||||
// Synopsis: Applies a transformation matrix to a description
|
||||
// Topics: Descriptions, Attachments
|
||||
// See Also: parent()
|
||||
// Usage:
|
||||
// new_desc = trans_desc(T, desc);
|
||||
// new_desc = transform_desc(T, desc);
|
||||
// Description:
|
||||
// Applies a transformation matrix to a description, producing a new transformed description as
|
||||
// output. The transformation matrix can be produced using any of the usual transform commands.
|
||||
@@ -5180,9 +5224,88 @@ function desc_dist(desc1,anchor1=CENTER, desc2, anchor2=CENTER)=
|
||||
// T = transformation or list of transformations to apply (a 4x4 matrix or list of them)
|
||||
// desc = description to transform
|
||||
|
||||
function trans_desc(T,desc) =
|
||||
function transform_desc(T,desc) =
|
||||
assert(is_description(desc), "Invalid description")
|
||||
is_consistent(T, ident(4)) ? [for(t=T) [t*desc[0], desc[1]]]
|
||||
: is_matrix(T,4,4) ? [T*desc[0], desc[1]]
|
||||
: assert(false,"T must be a 4x4 matrix or list of 4x4 matrices");
|
||||
|
||||
|
||||
// Module: desc_copies()
|
||||
// Synopsis: Places copies according to a list of transformation matrices and supplies descriptions for the copies.
|
||||
// SynTags: MatList, Trans
|
||||
// Topics: Transformations, Distributors, Copiers, Descriptions
|
||||
// See Also: line_copies(), move_copies(), xcopies(), ycopies(), zcopies(), grid_copies(), xflip_copy(), yflip_copy(), zflip_copy(), mirror_copy()
|
||||
// Usage:
|
||||
// desc_copies(transforms) CHILDREN;
|
||||
// Description:
|
||||
// Makes a copy of the children and applies each matrix in the list of transformation matrices.
|
||||
// This is equivalent to running `multmatrix()` over all the transformations for the children.
|
||||
// This function provides a method for working with descriptions of the whole set of copies by
|
||||
// making all of their descriptions available to the children. This functionality will primarly
|
||||
// be useful when the transformation consists only of translations and rotations and hence
|
||||
// does not change the size or shape of the children. If you change the shape of the objects, care
|
||||
// is required to ensure that the descriptions match correctly.
|
||||
// .
|
||||
// In a child object you obtain its description using {{parent()}} as usual. Once you have
|
||||
// that description you can also access descriptions of the other objects, assuming they have
|
||||
// identical geometry. (The geometry can vary if you make your object conditional on `$idx` for example.)
|
||||
// To get the next object use `$next()` and to get the previous one use `$prev()`. You can also
|
||||
// get an arbitrary object description by index using `$desc(i)`. You can use these descriptions
|
||||
// with {{prism_connector()}} to create prisms between the corresponding objects.
|
||||
// .
|
||||
// Note that in OpenSCAD version 2021.01 you cannot directly call `$next` or the other `$` functions.
|
||||
// You have to write `let(next=$next)` and then you can use the `next()` function. Similar steps
|
||||
// are necessary for the other functions. In development versions you can directly invoke `$next()`
|
||||
// and the other functions.
|
||||
// .
|
||||
// The descriptions are made available through function literals provided in the `$` variables. The
|
||||
// available functions are
|
||||
// * $next([di], [desc]): Returns the description of the next object, or if i is given, the object i steps forward. The indexing wraps around.
|
||||
// * $prev([di], [desc]): Returns the description of the previoud object, or if i is given, the object i steps before. The indexing wraps around.
|
||||
// * $desc(i, [desc]): Returns a description of the object with index `i`. Indexing does not wrap around.
|
||||
// All of these functions have an optional `desc` parameter, which is the description that will be transformed to produce the next, previous, or indexed
|
||||
// description. By default `desc` is set to {{parent()}}, but you may wish to use a different description if you have objects that vary.
|
||||
// .
|
||||
// See the last examples in {{prism_connector()}} for examples using this module.
|
||||
// Arguments:
|
||||
// transforms = list of transformation matrices to apply to the children
|
||||
// Side Effects:
|
||||
// `$count` is set to the number of transformations
|
||||
// `$idx` is set to the index number of the current transformation
|
||||
// `$is_last` is set to true if this is the last copy and false otherwise
|
||||
// `$next()` is set to a function literal that produces the next description (see above)
|
||||
// `$prev()` is set to a function literal that produces the previous description (see above)
|
||||
// `$desc()` is set to a function literal that produces the description at a specified index (see above)
|
||||
|
||||
module desc_copies(transforms)
|
||||
{
|
||||
$count=len(transforms);
|
||||
for(i=idx(transforms))
|
||||
let(
|
||||
$idx=i,
|
||||
$is_last = i==len(transforms)-1,
|
||||
$desc = function(i,desc) transform_desc(transforms[i]*matrix_inverse(transforms[i]),default(desc,parent())),
|
||||
$next = function(di=1,desc) transform_desc(select(transforms,i+di)*matrix_inverse(transforms[i]), default(desc,parent())),
|
||||
$prev = function(di=1,desc) transform_desc(select(transforms,i-di)*matrix_inverse(transforms[i]), default(desc,parent()))
|
||||
)
|
||||
multmatrix(transforms[i])children();
|
||||
}
|
||||
|
||||
|
||||
// Function: is_description()
|
||||
// Synopsis: Check if its argument is a descriptioni
|
||||
// Topics: Descriptions
|
||||
// Usage:
|
||||
// bool = is_description(desc);
|
||||
// Description:
|
||||
// Returns true if the argument appears to be a description.
|
||||
// Arguments:
|
||||
// desc = argument to check
|
||||
function is_description(desc) =
|
||||
is_list(desc) && len(desc)==2 && is_matrix(desc[0],4,4) && is_list(desc[1]) && is_string(desc[1][0]);
|
||||
|
||||
|
||||
|
||||
|
||||
// vim: expandtab tabstop=4 shiftwidth=4 softtabstop=4 nowrap
|
||||
|
||||
@@ -1243,8 +1243,8 @@ module arc_copies(
|
||||
ry = get_radius(r1=ry, r=r, d1=dy, d=d, dflt=1);
|
||||
sa = posmod(sa, 360);
|
||||
ea = posmod(ea, 360);
|
||||
n = (abs(ea-sa)<0.01)?(n+1):n;
|
||||
delt = (((ea<=sa)?360.0:0)+ea-sa)/(n-1);
|
||||
extra_n = (abs(ea-sa)<0.01)?1:0;
|
||||
delt = (((ea<=sa)?360.0:0)+ea-sa)/(n-1+extra_n);
|
||||
for ($idx = [0:1:n-1]) {
|
||||
$ang = sa + ($idx * delt);
|
||||
$pos =[rx*cos($ang), ry*sin($ang), 0];
|
||||
@@ -1271,8 +1271,8 @@ function arc_copies(
|
||||
ry = get_radius(r1=ry, r=r, d1=dy, d=d, dflt=1),
|
||||
sa = posmod(sa, 360),
|
||||
ea = posmod(ea, 360),
|
||||
n = (abs(ea-sa)<0.01)?(n+1):n,
|
||||
delt = (((ea<=sa)?360.0:0)+ea-sa)/(n-1),
|
||||
extra_n = (abs(ea-sa)<0.01)?1:0,
|
||||
delt = (((ea<=sa)?360.0:0)+ea-sa)/(n-1+extra_n),
|
||||
mats = [
|
||||
for (i = [0:1:n-1])
|
||||
let(
|
||||
|
||||
@@ -302,9 +302,9 @@ module stroke(
|
||||
attachable(){
|
||||
for (path = paths) {
|
||||
pathvalid = is_path(path,[2,3]) || same_shape(path,[[0,0]]) || same_shape(path,[[0,0,0]]);
|
||||
assert(pathvalid,"The path argument must be a list of 2D or 3D points, or a region.");
|
||||
|
||||
check4 = assert(is_num(width) || len(width)==len(path),
|
||||
check4 = assert(pathvalid,"The path argument must be a list of 2D or 3D points, or a region.")
|
||||
assert(is_num(width) || len(width)==len(path),
|
||||
"width must be a number or a vector the same length as the path (or all components of a region)");
|
||||
path = deduplicate( closed? list_wrap(path) : path );
|
||||
width = is_num(width)? [for (x=path) width]
|
||||
@@ -1233,7 +1233,8 @@ function _turtle_command(command, parm, parm2, state, index) =
|
||||
radius = parm*sign(myangle),
|
||||
center = lastpt + lrsign*radius*line_normal([0,0],state[step]),
|
||||
steps = state[arcsteps]==0 ? segs(abs(radius)) : state[arcsteps],
|
||||
arcpath = myangle == 0 || radius == 0 ? [] : arc(
|
||||
arcpath = myangle == 0 || radius == 0 ? []
|
||||
: arc(
|
||||
steps,
|
||||
points = [
|
||||
lastpt,
|
||||
|
||||
@@ -41,9 +41,10 @@ function _is_point_on_line(point, line, bounded=false, eps=EPSILON) =
|
||||
v1 = (line[1]-line[0]),
|
||||
v0 = (point-line[0]),
|
||||
t = v0*v1/(v1*v1),
|
||||
bounded = force_list(bounded,2)
|
||||
bounded = force_list(bounded,2),
|
||||
norm_crossprod = len(v1)==2 ? abs(cross(v0,v1)) : norm(cross(v0,v1))
|
||||
)
|
||||
abs(cross(v0,v1))<=eps*norm(v1)
|
||||
norm_crossprod <= eps*norm(v1)
|
||||
&& (!bounded[0] || t>=-eps)
|
||||
&& (!bounded[1] || t<1+eps) ;
|
||||
|
||||
@@ -904,6 +905,48 @@ function _is_point_above_plane(plane, point) =
|
||||
point_plane_distance(plane, point) > EPSILON;
|
||||
|
||||
|
||||
// Module: show_plane()
|
||||
// Synopsis: Display (part of) a plane
|
||||
// SynTags: Geom
|
||||
// Topics: Planes
|
||||
// Usage:
|
||||
// show_plane(plane, size, [offset]) [ATTACHMENTS];
|
||||
// Description:
|
||||
// Display a rectangular portion of the specified plane for debugging or visualization purposes.
|
||||
// The size parameter specifies the size of the plane when projected along the coordinate axis that is closest to
|
||||
// the plane's normal vector. The offset parameter will shift the plane location perpendicular to the normal vector.
|
||||
// This object is a non-manifold VNF (it has edges) so it will not render.
|
||||
// Arguments:
|
||||
// plane = Plane to display
|
||||
// size = scalar or 2-vector size parameter
|
||||
// offset = scalar of 2-vector offset
|
||||
// Example(3D):
|
||||
// sphere(r=15,$fn=48);
|
||||
// plane = plane_from_normal([2,-3,9],[4,-5,12]);
|
||||
// %show_plane(plane, [35,25], [4,-7]);
|
||||
|
||||
module show_plane(plane, size, offset=0)
|
||||
{
|
||||
size = force_list(size,2);
|
||||
offset = force_list(offset, 2, 0);
|
||||
checks =
|
||||
assert(is_vector(size,2), "The size parameter must be a scalar or 2-vector")
|
||||
assert(is_vector(offset,2), "The offset parameter must be a scalar or 2-vector");
|
||||
pts = move(offset,rect(size));
|
||||
axes = [UP, BACK, RIGHT];
|
||||
n = plane_normal(plane);
|
||||
ang = [for(v=axes) abs(plane_line_angle(plane, [CTR,v]))];
|
||||
axis = axes[max_index(ang)];
|
||||
face = [for(pt=pts)
|
||||
axis==UP? [pt.x,pt.y,(plane[3]-plane.x*pt.x-plane.y*pt.y)/plane.z]
|
||||
: axis==BACK? [pt[0],(plane[3]-plane.x*pt[0]-plane.z*pt[1])/plane.y,pt[1]]
|
||||
: [(plane[3]-plane.y*pt[0]-plane.z*pt[1])/plane.x,pt[0],pt[1]]
|
||||
];
|
||||
vnf = [face, [count(face)]];
|
||||
vnf_polyhedron(vnf) children();
|
||||
}
|
||||
|
||||
|
||||
|
||||
// Section: Circle Calculations
|
||||
|
||||
|
||||
BIN
images/metaball_demo2d.gif
Normal file
BIN
images/metaball_demo2d.gif
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 1.0 MiB |
@@ -1648,7 +1648,6 @@ function debug_tetra(r) = let(size=r/norm([1,1,1])) [
|
||||
|
||||
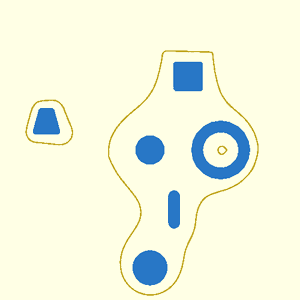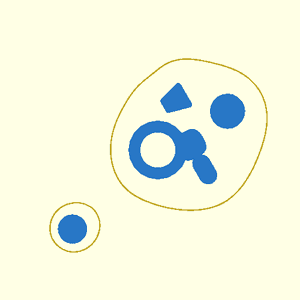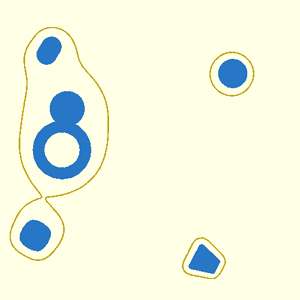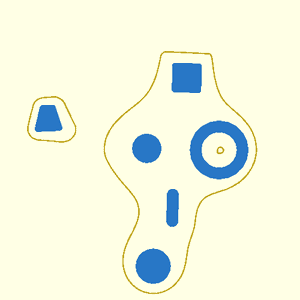
// Section: Metaballs
|
||||
// 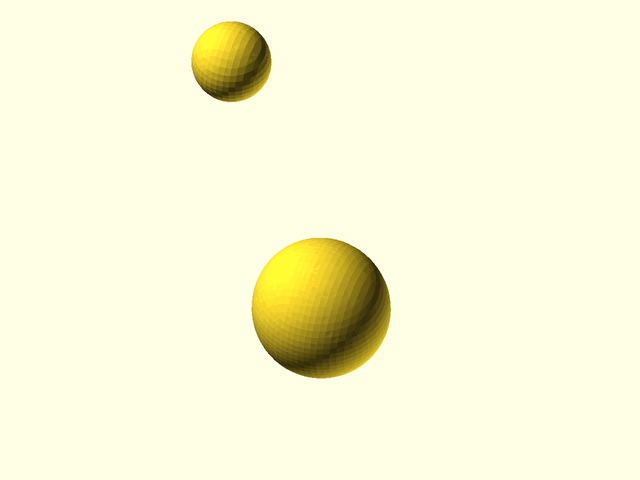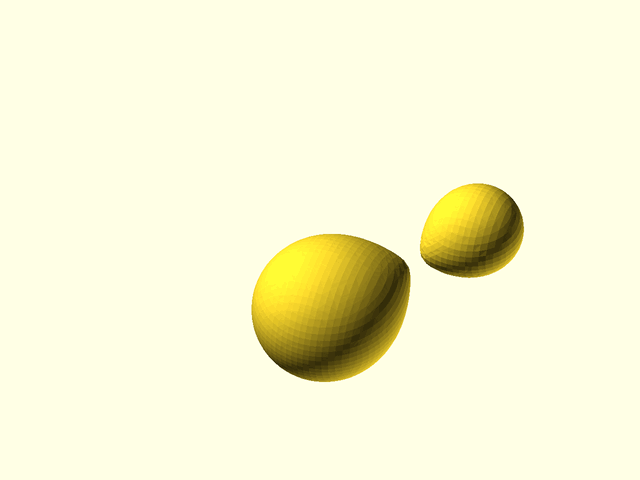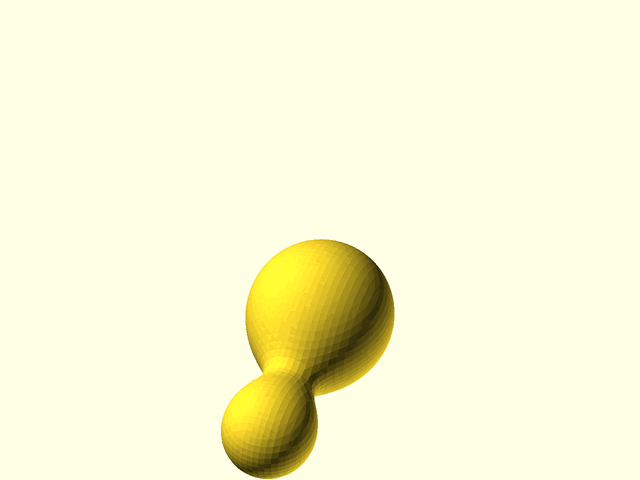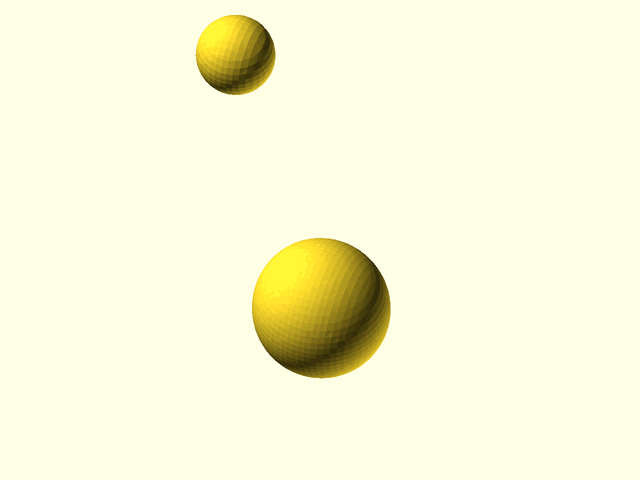
|
||||
// 
|
||||
// .
|
||||
// [Metaballs](https://en.wikipedia.org/wiki/Metaballs), also known as "blobby objects",
|
||||
// can produce smoothly varying blobs and organic forms. You create metaballs by placing metaball
|
||||
@@ -2653,13 +2652,13 @@ function mb_stadium(size, cutoff=INF, influence=1, negative=false, hide_debug=fa
|
||||
length = shape>=0 ? siz[1] : siz[0],
|
||||
r = shape>=0 ? siz[0]/2 : siz[1]/2,
|
||||
sl = length-2*r, // straight side length
|
||||
dum3 = assert(sl>0, "\nTotal length must accommodate rounded ends of rectangle."),
|
||||
//dum3 = assert(sl>=0, "\nTotal length must accommodate rounded ends of rectangle."),
|
||||
neg = negative ? -1 : 1,
|
||||
poly = shape<=EPSILON ? [neg, hide_debug ? circle(r=0.02, $fn=3) : circle(r=r, $fn=20)]
|
||||
poly = abs(shape)<=EPSILON ? [neg, hide_debug ? circle(r=0.02, $fn=3) : circle(r=r, $fn=20)]
|
||||
: shape>0 ? [neg, hide_debug ? square(0.02,center=true) : rect([2*r,length], rounding=0.999*r, $fn=20)]
|
||||
: [neg, hide_debug ? square(0.02,center=true) : rect([length,2*r], rounding=0.999*r, $fn=20)]
|
||||
) abs(shape)<EPSILON ?
|
||||
[function (dv) _mb_circle_full(point, r, cutoff, 1/influence, neg), poly]
|
||||
[function (dv) _mb_circle_full(dv, r, cutoff, 1/influence, neg), poly]
|
||||
: shape>0 ? [function (dv) _mb_stadium_full(dv, sl/2, r, cutoff, 1/influence, neg), poly]
|
||||
: [function (dv) _mb_stadium_sideways_full(dv, sl/2, r, cutoff, 1/influence, neg), poly];
|
||||
|
||||
@@ -2719,6 +2718,8 @@ function mb_ring(r1,r2, cutoff=INF, influence=1, negative=false, hide_debug=fals
|
||||
// Usage: As a function
|
||||
// region = metaballs2d(spec, bounding_box, pixel_size, [isovalue=], [closed=], [use_centers=], [smoothing=], [exact_bounds=], [show_stats=]);
|
||||
// Description:
|
||||
// 
|
||||
// .
|
||||
// 2D metaball shapes can be useful to create interesting polygons for extrusion. When invoked as a
|
||||
// module, a 2D metaball scene is displayed. When called as a function, a list containing one or more
|
||||
// [paths](paths.scad) is returned.
|
||||
@@ -2954,7 +2955,7 @@ function mb_ring(r1,r2, cutoff=INF, influence=1, negative=false, hide_debug=fals
|
||||
module metaballs2d(spec, bounding_box, pixel_size, pixel_count, isovalue=1, use_centers=false, smoothing=undef, exact_bounds=false, convexity=6, cp="centroid", anchor="origin", spin=0, atype="hull", show_stats=false, show_box=false, debug=false) {
|
||||
regionlist = metaballs2d(spec, bounding_box, pixel_size, pixel_count, isovalue, true, use_centers, smoothing, exact_bounds, show_stats, _debug=debug);
|
||||
$metaball_pathlist = debug ? regionlist[0] : regionlist; // for possible use with children
|
||||
wid = min(0.5, 0.25 * (is_num(pixel_size) ? pixel_size : 0.5*(pixel_size[0]+pixel_size[1])));
|
||||
wid = min(0.5, 0.5 * (is_num(pixel_size) ? pixel_size : 0.5*(pixel_size[0]+pixel_size[1])));
|
||||
if(debug) {
|
||||
// display debug polygons
|
||||
for(a=regionlist[1])
|
||||
@@ -3259,7 +3260,7 @@ function _metaballs2dfield(funclist, transmatrix, bbox, pixsize, nballs) = let(
|
||||
// (x*y*z^3 - 3*x^2*z^2) / np^2 + np^2,
|
||||
// isovalue=[-INF,35], bounding_box=[[-32,-32,-14],[32,32,14]],
|
||||
// voxel_size = 0.8, show_box=true);
|
||||
// Example(3D,Med,NoAxes,VPD=47,VPT=[0,0,2]): You can specify non-cubical voxels for efficiency. This example shows the result of two identical surface functions. The figure on the left uses a `voxel_size=1`, which washes out the detail in the z direction. The figure on the right shows the same shape with `voxel_size=[0.5,1,0.2]` to give a bit more resolution in the x direction and much more resolution in the z direction. This example runs about six times faster than if we used a cubical voxel of size 0.2 to capture the detail in only one axis at the expense of unnecessary detail in other axes.
|
||||
// Example(3D,Med,NoAxes,VPD=47,VPT=[0,0,2]): You can specify non-cubical voxels for efficiency. This example shows the result of two identical surface functions. The figure on the left uses `voxel_size=1`, which washes out the detail in the z direction. The figure on the right shows the same shape with `voxel_size=[0.5,1,0.2]` to give a bit more resolution in the x direction and much more resolution in the z direction. This example runs about six times faster than if we used a cubical voxel of size 0.2 to capture the detail in only one axis at the expense of unnecessary detail in other axes.
|
||||
// function shape(x,y,z, r=5) =
|
||||
// r / sqrt(x^2 + 0.5*(y^2 + z^2) + 0.5*r*cos(200*z));
|
||||
// bbox = [[-6,-8,0], [6,8,7]];
|
||||
@@ -3478,18 +3479,11 @@ function _showstats_isosurface(voxsize, bbox, isoval, cubes, triangles, faces) =
|
||||
// .
|
||||
// When `closed=false`, paths that intersect the edge of the bounding box end at the bounding box. This
|
||||
// means that the list of paths may include a mixture of closed and open paths. Regardless of whether
|
||||
// any of the output paths are open, all closed paths have identical first and last points so that closed and open paths can be distinguished. You can use {{are_ends_equal()}} to determine if a path is closed. A path list that includes open paths is not a region, since regions are lists of closed polygons. Duplicating the ends of closed paths can cause problems for some functions such as {{offset()}} which will complain about repeated points; to deal with this problem you can pass the closed components to {{list_unwrap()}} to remove the extra endpoint.
|
||||
|
||||
|
||||
// The parameter `closed=true` is set by default, which causes polygon segments to be generated wherever a
|
||||
// contour is clipped by the bounding box, so that all contours are closed polygons. When `closed=true`,
|
||||
// the list of paths returned by `contour()` is a valid [region](regions.scad) with no duplicated
|
||||
// vertices in any path, and all paths are treated as as closed polygons by the `contour()` module.
|
||||
// When calling `contour()` as a module, the `closed` parameter is unavailable and always true.
|
||||
// .
|
||||
// When `closed=false`, however, the list of paths returned by the `contour()` function may include a
|
||||
// mixture of closed and unclosed paths, in which the closed paths can be identified as having equivalent
|
||||
// start and end points (this duplication makes the path list an invalid [region](regions.scad)).
|
||||
// any of the output paths are open, all closed paths have identical first and last points so that closed and
|
||||
// open paths can be distinguished. You can use {{are_ends_equal()}} to determine if a path is closed. A path
|
||||
// list that includes open paths is not a region, because regions are lists of closed polygons. Duplicating the
|
||||
// ends of closed paths can cause problems for functions such as {{offset()}}, which would complain about
|
||||
// repeated points. You can pass a closed path to {{list_unwrap()}} to remove the extra endpoint.
|
||||
// Arguments:
|
||||
// f = The contour function or array.
|
||||
// isovalue = a scalar giving the isovalue parameter.
|
||||
|
||||
791
rounding.scad
791
rounding.scad
@@ -1374,7 +1374,7 @@ module offset_stroke(path, width=1, rounded=true, start, end, check_valid=true,
|
||||
// - smooth: os_smooth(cut|joint, [k]). Define continuous curvature rounding, with `cut` and `joint` as for round_corners. The k parameter controls how fast the curvature changes and should be between 0 and 1.
|
||||
// - teardrop: os_teardrop(r|cut). Rounding using a 1/8 circle that then changes to a 45 degree chamfer. The chamfer is at the end, and enables the object to be 3d printed without support. The radius gives the radius of the circular part.
|
||||
// - chamfer: os_chamfer([height], [width], [cut], [angle]). Chamfer the edge at desired angle or with desired height and width. You can specify height and width together and the angle is ignored, or specify just one of height and width and the angle is used to determine the shape. Alternatively, specify "cut" along with angle to specify the cut back distance of the chamfer.
|
||||
// - mask: os_mask(mask, [out]). Create a profile from one of the [2d masking shapes](shapes2d.scad#5-2d-masking-shapes). The `out` parameter specifies that the mask should flare outward (like crown molding or baseboard). This is set false by default.
|
||||
// - mask: os_mask(mask, [out]). Create a profile from one of the [2d masking shapes](shapes2d.scad#section-2d-masking-shapes). The `out` parameter specifies that the mask should flare outward (like crown molding or baseboard). This is set false by default.
|
||||
// .
|
||||
// The general settings that you can use with all of the helper functions are mostly used to control how offset_sweep() calls the offset() function.
|
||||
// - extra: Add an extra vertical step of the specified height, to be used for intersections or differences. This extra step extends the resulting object beyond the height you specify. It is ignored by anchoring. Default: 0
|
||||
@@ -2190,7 +2190,7 @@ function _rp_compute_patches(top, bot, rtop, rsides, ktop, ksides, concave) =
|
||||
// "prismoid" = For four sided prisms only, defined standard prismsoid anchors, with RIGHT set to the face closest to the RIGHT direction.
|
||||
// Example: Uniformly rounded pentagonal prism
|
||||
// rounded_prism(pentagon(3), height=3,
|
||||
// joint_top=0.5, joint_bot=0.5, joint_sides=0.5);
|
||||
// joint_top=0.5, joint_bot=0.5, joint_sides=0.5) position(FWD) cube(1);
|
||||
// Example: Maximum possible rounding.
|
||||
// rounded_prism(pentagon(3), height=3,
|
||||
// joint_top=1.5, joint_bot=1.5, joint_sides=1.5);
|
||||
@@ -2860,7 +2860,8 @@ Access to the derivative smoothing parameter?
|
||||
// For the cylinder and spherical objects you may wish to joint a prism to the concave surface. You can do this by setting a negative
|
||||
// radius for the base or auxiliary object. When `base_r` is negative, and the joiner prism axis is vertical, the prism root is **below** the
|
||||
// XY plane. In this case it is actually possible to use the same object for base and aux and you can get a joiner prism that crosses a cylindrical
|
||||
// or spherical hole.
|
||||
// or spherical hole. You can also attach to the inside of a prism object by setting the corresponding radius to a negative value. Only the sign
|
||||
// matters in this case.
|
||||
// .
|
||||
// When placing prisms inside a hole, an ambiguity can arise about how to identify the root and end of the joiner prism. The prism axis has
|
||||
// two intersections with a cylinder and both are potentially valid roots. When the auxiliary object is entirely inside the hole, or the auxiliary
|
||||
@@ -2876,6 +2877,11 @@ Access to the derivative smoothing parameter?
|
||||
// to achieve the specified length (if aux is "none") or to contact the auxiliary object, if you have specified one. This means, for example,
|
||||
// that setting `prism_end_T` to a scale operation doesn't change the result because it doesn't alter the prism axis.
|
||||
// .
|
||||
// A different way to specify the prism position is using the `start` and `end` parameters, which specify the axis of the prism's centerline.
|
||||
// You cannot combine `prism_end_T` with either `start` or `end`. if you give only `start` then the prism's anchor point on the base
|
||||
// will be shifted but its direction will remain the same. If you give only `end` then the prism's anchor point on the base remains
|
||||
// fixed (as computed based on the center-to-center line) and only the point on the auxiliary object moves.
|
||||
// .
|
||||
// The size of the fillets is determined by the fillet, `fillet_base`, and `fillet_aux` parameters. The fillet parameter controls both
|
||||
// ends of the prism, or you can set the ends independently. The fillets must be nonnegative except when the prism joints a plane.
|
||||
// In this case a negative fillet gives a roundover. In the case of no auxiliary object you can use `round_end` to round over the planar
|
||||
@@ -2888,6 +2894,14 @@ Access to the derivative smoothing parameter?
|
||||
// For joins to convex objects you can choose a small value, but when joining to a concave object the overlap may need to be
|
||||
// large to ensure that the base of the joiner prism is well-behaved. In such cases you may need to use an intersection
|
||||
// remove excess base.
|
||||
// .
|
||||
// When connecting to a base or auxiliary object that is a prism, the `smooth_normals` parameter controls how normals on that prism are
|
||||
// computed. If `smooth_normals=true` (the default) then the normals are interpolated across the faces to create a more continuously varying normal.
|
||||
// This generally produces good results if the prism is a continous shape that is uniformly and finely sampled. But if the shape has
|
||||
// large faces it can produce inferior or even incorrect results. For example, {{prism_connector()}} makes connections to edges of objects
|
||||
// and must set `smooth_normals=false` to get correct results in this situation, or the constructed prism ends up hidden inside the object in
|
||||
// joins to. If you create a prism that appears to suffer from this problem an informational (nonfatal) message will be displayed.
|
||||
// Note that the messages appears once for every problematic point in your joining profile.
|
||||
// Figure(2D,Med,NoAxes): Uniform fillet method. This image shows how we construct a uniform fillet. The pictures shows the cross section that is perpendicular to the prism. The blue curve represents the base object surface. The vertical line is the side of the prism. To construct a fillet we travel along the surface of the base, following the curve, until we have moved the fillet length, `a`. This defines the point `u`. We then construct a tangent line to the base and find its intersection, `v`, with the prism. Note that if the base is steeply curved, this tangent may fail to intersect, and the algorithm fails with an error because `v` does not exist. Finally we locate `w` to be distance `a` above the point where the prism intersects the base object. The fillet is defined by the `[u,v,w]` triple and is shown in red. Note that with this method, the fillet is always height `a` above the base, so it makes a uniform curve parallel to the base object. However, when the base curvature is more extreme, point `v` may end up above point `w`, resulting in an invalid configuration. It also happens that point `v`, while below `w`, is close to `w`, so the resulting fillet has an abrupt angle near `w` instead of a smooth transition.
|
||||
// R=60;
|
||||
// base = R*[cos(70),sin(70)];
|
||||
@@ -2960,6 +2974,8 @@ Access to the derivative smoothing parameter?
|
||||
// aux = string specifying auxilary object to connect to ("none", "plane", "cyl", "cylinder", or "sphere") or a point list to use an arbitrary prism. Default: "none"
|
||||
// aux_T = rotation operator that may include translation when aux is not "none" to apply to aux
|
||||
// aux_r / aux_d = radius or diameter of auxiliary object if you picked sphere or cylinder
|
||||
// start = starting endpoint for the axis of the prism center
|
||||
// end = ending endpoint for the axis of the prism center
|
||||
// n = number of segments in the fillet at both ends. Default: 15
|
||||
// base_n = number of segments to use in fillet at the base
|
||||
// aux_n = number of segments to use in fillet at the aux object
|
||||
@@ -2977,6 +2993,9 @@ Access to the derivative smoothing parameter?
|
||||
// uniform = set to false to get non-uniform filleting at both ends (see Figures 2-3). Default: true
|
||||
// base_uniform = set to false to get non-uniform filleting at the base
|
||||
// aux_uniform = set to false to get non-uniform filleting at the auxiliary object
|
||||
// smooth_normals = if true then smooth normals to the base and auxiliary objects when those objects are prisms. If false do not smooth the normals. No effect for objects that are not prisms. Default: true
|
||||
// base_smooth_normals = set to true or false to control smoothing of normals on the base prism object only
|
||||
// aux_smooth_normals = set to true or false to control smoothing of normals on the auxiliary prism object only
|
||||
// debug = set to true to allow return of various cases where self-intersection was detected
|
||||
// anchor = Translate so anchor point is at the origin. (module only) Default: "origin"
|
||||
// spin = Rotate this many degrees around Z axis after anchor. (module only) Default: 0
|
||||
@@ -3103,7 +3122,7 @@ Access to the derivative smoothing parameter?
|
||||
// sphere(r=30,$fn=64);
|
||||
// }
|
||||
// }
|
||||
// Example(3D,NoScales,VPD=126,VPR=[55,0,25],VPT=[1.23541,-1.80334,-16.9789]): Here is an example with a spherical base. This overlap is near the minimum required to eliminate the gap, but it creates a large excess structure around the base of the prism.
|
||||
// Example(3D,NoScales,VPD=126,VPR=[55,0,25],VPT=[1.23541,-1.80334,-16.9789]): Here is the previous example with the excess structure differenced away.
|
||||
// flower = [for(theta=lerpn(0,360,180,endpoint=false))
|
||||
// (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]];
|
||||
// intersection(){
|
||||
@@ -3277,6 +3296,14 @@ Access to the derivative smoothing parameter?
|
||||
// fillet=3, n=25);
|
||||
// linear_sweep(1.4*flower,height=60,center=true,
|
||||
// convexity=10,orient=RIGHT);
|
||||
// Example(3D,NoScales): The same example as above with `smooth_normals=false` produces a banding pattern in the fillet.
|
||||
// flower = [for(theta=lerpn(0,360,180,endpoint=false))
|
||||
// (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]];
|
||||
// join_prism(flower,base=1.4*flower, length=20,
|
||||
// prism_end_T=yrot(20),aux_T=xrot(10),
|
||||
// fillet=3, n=25,smooth_normals=false);
|
||||
// linear_sweep(1.4*flower,height=60,center=true,
|
||||
// convexity=10,orient=RIGHT);
|
||||
// Example(3D,NoScales,VPR=[78,0,42],VPT=[12.45,-12.45,10.4],VPD=130): Instead of terminating your prism in a flat face perpendicular to its axis you can attach it to a second object. The simplest case is to connect to planar attachments. When connecting to a second object you must position and orient the second object using aux_T, which is now allowed to be a rotation and translation operator. The `length` parameter is no longer allowed.
|
||||
// flower = [for(theta=lerpn(0,360,180,endpoint=false))
|
||||
// (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]];
|
||||
@@ -3446,8 +3473,9 @@ module join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
fillet, base_fillet,aux_fillet,end_round,
|
||||
k=0.7, base_k,aux_k,end_k,start,end,
|
||||
uniform=true, base_uniform, aux_uniform,
|
||||
smooth_normals=true, base_smooth_normals, aux_smooth_normals,
|
||||
debug=false, anchor="origin", extent=true, cp="centroid", atype="hull", orient=UP, spin=0,
|
||||
convexity=10)
|
||||
convexity=10,_name1="base",_name2="aux")
|
||||
{
|
||||
assert(in_list(atype, _ANCHOR_TYPES), "Anchor type must be \"hull\" or \"intersect\"");
|
||||
vnf_start_end = join_prism(polygon,base, base_r=base_r, base_d=base_d, base_T=base_T,
|
||||
@@ -3460,7 +3488,8 @@ module join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
k=k, base_k=base_k, aux_k=aux_k, end_k=end_k,
|
||||
uniform=uniform, base_uniform=base_uniform, aux_uniform=aux_uniform,
|
||||
debug=debug, start=start, end=end,
|
||||
return_axis=true
|
||||
smooth_normals=smooth_normals, base_smooth_normals=base_smooth_normals, aux_smooth_normals=aux_smooth_normals,
|
||||
return_axis=true, _name1=_name1, _name2=_name2
|
||||
);
|
||||
axis = vnf_start_end[2] - vnf_start_end[1];
|
||||
anchors = [
|
||||
@@ -3484,7 +3513,9 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
fillet, base_fillet,aux_fillet,end_round,
|
||||
k=0.7, base_k,aux_k,end_k,
|
||||
uniform=true, base_uniform, aux_uniform,
|
||||
debug=false, return_axis=false, start, end) =
|
||||
debug=false, return_axis=false,
|
||||
smooth_normals=true, base_smooth_normals, aux_smooth_normals,
|
||||
start, end, _name1="base", _name2="aux") =
|
||||
let(
|
||||
objects=["cyl","cylinder","plane","sphere"],
|
||||
length = one_defined([h,height,l,length], "h,height,l,length", dflt=undef)
|
||||
@@ -3516,7 +3547,10 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
base_overlap = one_defined([base_overlap,overlap],"base_overlap,overlap",base_fillet>0?1:0),
|
||||
aux_overlap = one_defined([aux_overlap,overlap],"aux_overlap,overlap",aux_fillet>0?1:0),
|
||||
base_uniform = first_defined([base_uniform, uniform]),
|
||||
aux_uniform = first_defined([aux_uniform, uniform])
|
||||
aux_uniform = first_defined([aux_uniform, uniform]),
|
||||
base_smooth_normals = first_defined([base_smooth_normals, smooth_normals]),
|
||||
aux_smooth_normals = first_defined([aux_smooth_normals, smooth_normals])
|
||||
|
||||
)
|
||||
assert(is_num(base_fillet),"Must give a numeric fillet or base_fillet value")
|
||||
assert(base=="plane" || base_fillet>=0, "Fillet for non-planar base object must be nonnegative")
|
||||
@@ -3526,7 +3560,8 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
assert(!in_list(aux,["sphere","cyl","cylinder"]) || (is_num(aux_r) && !approx(aux_r,0)), str("Must give nonzero aux_r with base ",base))
|
||||
assert(!short || (in_list(base,["sphere","cyl","cylinder"]) && base_r<0), "You can only set short to true if the base is a sphere or cylinder with radius<0")
|
||||
let(
|
||||
base_r=default(base_r,0),
|
||||
base_r=default(base_r,1),
|
||||
aux_r=default(aux_r,1),
|
||||
polygon=clockwise_polygon(polygon),
|
||||
start_center = CENTER,
|
||||
aux_T_horiz = submatrix(aux_T,[0:2],[0:2]) == ident(3) && aux_T[2][3]==0,
|
||||
@@ -3553,7 +3588,7 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
: is_path(base) ?
|
||||
let(
|
||||
mapped = apply(yrot(-90),axisline),
|
||||
answer = _prism_line_isect(pair(base,wrap=true),mapped,mapped[1])[0]
|
||||
answer = _prism_line_isect(pair(base,wrap=true),mapped,sign(base_r)*mapped[1])[0]
|
||||
)
|
||||
assert(answer,"Prism center doesn't intersect prism (base)")
|
||||
apply(yrot(90),answer)
|
||||
@@ -3563,7 +3598,7 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
prism_end_T = aux=="none" ? IDENT : prism_end_T,
|
||||
aux = aux=="none" && aux_fillet!=0 ? "plane" : aux,
|
||||
end_center = apply(aux_T,CENTER),
|
||||
ndir = base_r<0 ? unit(start_center-start) : unit(end_center-start_center,UP),
|
||||
ndir = base_r<0 && in_list(base,["cylinder","cyl","sphere"]) ? unit(start_center-start) : unit(end_center-start_center,UP),
|
||||
end_prelim = is_def(end) ? end
|
||||
:apply(move(start)*prism_end_T*move(-start),
|
||||
aux=="sphere" ?
|
||||
@@ -3580,7 +3615,7 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
: is_path(aux) ?
|
||||
let(
|
||||
mapped = apply(yrot(90),[start,start+ndir]),
|
||||
answer = _prism_line_isect(pair(aux,wrap=true),mapped,mapped[0]-mapped[1])[0]
|
||||
answer = _prism_line_isect(pair(aux,wrap=true),mapped,sign(aux_r)*(mapped[0]-mapped[1]))[0] //!!!
|
||||
)
|
||||
assert(answer,"Prism center doesn't intersect prism (aux)")
|
||||
apply(aux_T*yrot(-90),answer)
|
||||
@@ -3601,7 +3636,7 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
: is_path(aux) ?
|
||||
let(
|
||||
mapped = apply(yrot(90)*move(-end_center),[start,end_prelim]),
|
||||
answer = _prism_line_isect(pair(aux,wrap=true),mapped,mapped[0]-mapped[1])[0]
|
||||
answer = _prism_line_isect(pair(aux,wrap=true),mapped,sign(aux_r)*(mapped[0]-mapped[1]))[0]
|
||||
)
|
||||
assert(answer,"Prism center doesn't intersect prism (aux)")
|
||||
apply(move(end_center)*yrot(-90),answer)
|
||||
@@ -3612,11 +3647,11 @@ function join_prism(polygon, base, base_r, base_d, base_T=IDENT,
|
||||
base_trans = rot_inverse(base_T),
|
||||
base_top = apply(base_trans, truetop),
|
||||
base_bot = apply(base_trans, truebot),
|
||||
botmesh = apply(base_T,_prism_fillet("base", base, base_r, base_bot, base_top, base_fillet, base_k, base_n, base_overlap,base_uniform,debug)),
|
||||
botmesh = apply(base_T,_prism_fillet(_name1, base, base_r, base_bot, base_top, base_fillet, base_k, base_n, base_overlap,base_uniform,base_smooth_normals,debug)),
|
||||
aux_trans = rot_inverse(aux_T),
|
||||
aux_top = apply(aux_trans, reverse_polygon(truetop)),
|
||||
aux_bot = apply(aux_trans, reverse_polygon(truebot)),
|
||||
topmesh_reversed = _prism_fillet("aux",aux, aux_r, aux_top, aux_bot, aux_fillet, aux_k, aux_n, aux_overlap,aux_uniform,debug),
|
||||
topmesh_reversed = _prism_fillet(_name2,aux, aux_r, aux_top, aux_bot, aux_fillet, aux_k, aux_n, aux_overlap,aux_uniform,aux_smooth_normals,debug),
|
||||
topmesh = apply(aux_T,[for(i=[len(topmesh_reversed)-1:-1:0]) reverse_polygon(topmesh_reversed[i])]),
|
||||
round_dir = select(topmesh,-1)-botmesh[0],
|
||||
roundings_cross = [for(i=idx(truetop)) if (round_dir[i]*(truetop[i]-truebot[i])<0) i],
|
||||
@@ -3692,12 +3727,12 @@ function _prism_line_isect(poly_pairs, line, ref) =
|
||||
[point3d(isect2d,z),isect_ind, isect_u];
|
||||
|
||||
|
||||
function _prism_fillet(name, base, R, bot, top, d, k, N, overlap,uniform,debug) =
|
||||
function _prism_fillet(name, base, R, bot, top, d, k, N, overlap,uniform,smooth_normals, debug) =
|
||||
base=="none" ? [bot]
|
||||
: base=="plane" ? _prism_fillet_plane(name,bot, top, d, k, N, overlap,debug)
|
||||
: base=="cyl" || base=="cylinder" ? _prism_fillet_cyl(name, R, bot, top, d, k, N, overlap,uniform,debug)
|
||||
: base=="sphere" ? _prism_fillet_sphere(name, R, bot, top, d, k, N, overlap,uniform,debug)
|
||||
: is_path(base,2) ? _prism_fillet_prism(name, base, bot, top, d, k, N, overlap,uniform,debug)
|
||||
: is_path(base,2) ? _prism_fillet_prism(name, base, bot, top, d, k, N, overlap,uniform,smooth_normals, R, debug)
|
||||
: assert(false,"Unknown base type");
|
||||
|
||||
|
||||
@@ -3706,7 +3741,10 @@ function _prism_fillet_plane(name, bot, top, d, k, N, overlap,debug) =
|
||||
dir = sign(top[0].z-bot[0].z), // Negative if we are upside down, with "top" below "bot"
|
||||
isect = [for (i=idx(top)) plane_line_intersection([0,0,1,0], [top[i],bot[i]])]
|
||||
)
|
||||
d==0 ? [isect, if (overlap!=0) isect + overlap*dir*DOWN] :
|
||||
d==0 ? [isect,
|
||||
if (overlap!=0) isect,
|
||||
if (overlap!=0) move(overlap*dir*DOWN,isect),
|
||||
] :
|
||||
let(
|
||||
base_normal = -path3d(path_normals(path2d(isect), closed=true)),
|
||||
mesh = transpose([for(i=idx(top))
|
||||
@@ -3739,10 +3777,12 @@ function _prism_fillet_cyl(name, R, bot, top, d, k, N, overlap, uniform, debug)
|
||||
cisect
|
||||
]
|
||||
)
|
||||
d==0 ? [
|
||||
d==0 ? yrot(90,[
|
||||
isect,
|
||||
if (overlap!=0) isect,
|
||||
if (overlap!=0) [for(p=isect) point3d(unit(point2d(p))*(norm(point2d(p))-sign(R)*overlap),p.z)]
|
||||
] :
|
||||
])
|
||||
:
|
||||
let(
|
||||
tangent = path_tangents(isect,closed=true),
|
||||
mesh = transpose([for(i=idx(top))
|
||||
@@ -3787,6 +3827,7 @@ function _prism_fillet_sphere(name, R,bot, top, d, k, N, overlap, uniform, debug
|
||||
]
|
||||
)
|
||||
d==0 ? [isect,
|
||||
if (overlap!=0) isect,
|
||||
if (overlap!=0) [for(p=isect) p - overlap*sign(R)*unit(p)]
|
||||
] :
|
||||
let(
|
||||
@@ -3812,29 +3853,28 @@ function _prism_fillet_sphere(name, R,bot, top, d, k, N, overlap, uniform, debug
|
||||
each bezier_curve(bez, N, endpoint=true),
|
||||
if (overlap!=0) edgepoint - overlap*sign(R)*unit(edgepoint)
|
||||
]
|
||||
])
|
||||
]),
|
||||
test_profile = project_plane(plane_from_normal(centroid(top)-centroid(bot)), select(mesh,-2))
|
||||
)
|
||||
// this test fails if the prism isn't "vertical". Project along prism direction?
|
||||
assert(debug || is_path_simple(path2d(select(mesh,-2)),closed=true),str("Fillet doesn't fit: it intersects itself (",name,")"))
|
||||
assert(debug || is_path_simple(test_profile,closed=true),str("Fillet doesn't fit: it intersects itself (",name,")"))
|
||||
mesh;
|
||||
|
||||
|
||||
|
||||
// Return an interpolated normal to the polygon at segment i, fraction u along the segment.
|
||||
|
||||
function _getnormal(polygon,index,u,) =
|
||||
function _getnormal(polygon,index,u,smooth_normals) =
|
||||
let(
|
||||
//flat=1/3,
|
||||
flat=1/8,
|
||||
// flat=0,
|
||||
flat = smooth_normals ? 1/8 : 1, // Normals are interpolated between faces. The middle frac portion of each face gets the true face normal
|
||||
// and then interpolation starts at the end of the flat region. With flat=1 only endpoints are interpolated.
|
||||
edge = (1-flat)/2,
|
||||
L=len(polygon),
|
||||
next_ind = posmod(index+1,L),
|
||||
prev_ind = posmod(index-1,L),
|
||||
this_normal = line_normal(select(polygon,index,index+1))
|
||||
)
|
||||
u > 1-edge ? lerp(this_normal,line_normal(select(polygon,index+1,index+2)), (u-edge-flat)/edge/2)
|
||||
: u < edge ? lerp(line_normal(select(polygon,index-1,index)),this_normal, 0.5+u/edge/2)
|
||||
u >= 1-edge ? lerp(this_normal,line_normal(select(polygon,index+1,index+2)), edge==0? 0.5 : (u-edge-flat)/edge/2)
|
||||
: u <= edge ? lerp(line_normal(select(polygon,index-1,index)),this_normal, edge==0? 0.5 : 0.5+u/edge/2)
|
||||
: this_normal;
|
||||
|
||||
|
||||
@@ -3863,49 +3903,718 @@ function _polygon_step(poly, ind, u, dir, length) =
|
||||
|
||||
// This function needs more error checking?
|
||||
// Needs check for zero overlap case and zero joint case
|
||||
function _prism_fillet_prism(name, basepoly, bot, top, d, k, N, overlap, uniform, debug)=
|
||||
function _prism_fillet_prism(name, basepoly, bot, top, d, k, N, overlap, uniform, smooth_normals,inside, debug)=
|
||||
let(
|
||||
inside=sign(inside),
|
||||
top = yrot(-90,top),
|
||||
bot = yrot(-90,bot),
|
||||
basepoly = clockwise_polygon(basepoly),
|
||||
segpairs = pair(basepoly,wrap=true),
|
||||
isect_ind = [for (i=idx(top))
|
||||
let(isect = _prism_line_isect(segpairs, [top[i], bot[i]], top[i]))
|
||||
let(isect = _prism_line_isect(segpairs, [top[i], bot[i]], inside*top[i]))
|
||||
assert(isect, str("Prism doesn't fully intersect prism (",name,")"))
|
||||
isect
|
||||
],
|
||||
isect=column(isect_ind,0),
|
||||
index = column(isect_ind,1),
|
||||
uval = column(isect_ind,2),
|
||||
tangent = path_tangents(isect,closed=true),
|
||||
tangent = path_tangents(isect,closed=true)
|
||||
)
|
||||
d==0 ? yrot(90,[
|
||||
isect,
|
||||
if (overlap!=0) isect,
|
||||
if (overlap!=0)
|
||||
[for(i=idx(isect))
|
||||
let(normal = point3d(_getnormal(basepoly,index[i],uval[i],smooth_normals)))
|
||||
isect[i]-unit(point3d(normal))*overlap
|
||||
]
|
||||
])
|
||||
: let(
|
||||
mesh = transpose([for(i=idx(top))
|
||||
let(
|
||||
normal = point3d(_getnormal(basepoly,index[i],uval[i])),
|
||||
dir = unit(cross(normal,tangent[i])),
|
||||
normal = point3d(_getnormal(basepoly,index[i],uval[i],smooth_normals)),
|
||||
dir = inside*unit(cross(normal,tangent[i])),
|
||||
zpart = d*dir.z,
|
||||
length_needed = d*norm(point2d(dir)),
|
||||
edgept2d = _polygon_step(basepoly, index[i], uval[i], sign(cross(point2d(dir),point2d(normal))), length_needed),
|
||||
edgepoint = point3d(edgept2d[0],isect[i].z+zpart),
|
||||
corner = plane_line_intersection(plane_from_normal(point3d(_getnormal(basepoly, edgept2d[1],edgept2d[2])),edgepoint),
|
||||
corner = plane_line_intersection(plane_from_normal(point3d(_getnormal(basepoly, edgept2d[1],edgept2d[2],smooth_normals)),edgepoint),
|
||||
[top[i],isect[i]],
|
||||
bounded=false), // should be true!!! But fails to intersect if given true.
|
||||
d_step = abs(d)*unit(top[i]-isect[i])+(uniform?isect[i]:corner)
|
||||
bounded=false), // should be true, but fails to intersect sometimes at isect[i] end
|
||||
d_step = abs(d)*unit(top[i]-isect[i])+(uniform?isect[i]:corner),
|
||||
within_top = is_point_on_line(corner, [top[i],isect[i]], RAY),
|
||||
within_bottom = is_point_on_line(corner, [isect[i],top[i]], RAY, 1e-1), // Not sure what epsilon should be here, but 0.1 units under the object seems OK
|
||||
dummy = within_bottom ? 0
|
||||
: echo(str("Warning: fillet appears to be inside the ",name,
|
||||
" object. If so you can try changing 'smooth_normals' or 'uniform'"))
|
||||
)
|
||||
assert(is_vector(corner,3),str("Fillet does not fit. Decrease size of fillet (",name,")."))
|
||||
assert(debug || (top[i]-d_step)*(d_step-corner)>=0,
|
||||
assert(within_top,str("Fillet does not fit. Decrease size of fillet (",name,")."))
|
||||
assert(debug || (top[i]-d_step)*(d_step-isect[i])>=0,
|
||||
str("Unable to fit fillet, probably due to steep curvature of the prism (",name,").",
|
||||
d_step," ",corner," ", edgepoint," ", isect[i]
|
||||
d_step," ",corner," ", edgepoint," ", isect[i], " ", top[i]
|
||||
))
|
||||
let(
|
||||
bez = _smooth_bez_fill([d_step,corner,edgepoint], k)
|
||||
)
|
||||
[
|
||||
each bezier_curve(bez, N, endpoint=true),
|
||||
if (overlap!=0) edgepoint-point3d(normal)*overlap
|
||||
if (overlap!=0) edgepoint-unit(point3d(normal))*overlap*inside
|
||||
]
|
||||
])
|
||||
)
|
||||
yrot(90,mesh);
|
||||
|
||||
|
||||
|
||||
// Module: prism_connector()
|
||||
// Synopsis: Construct a filleted prism that connects objects
|
||||
// SynTags: Geom
|
||||
// Topics: Rounding, Extrusion, Sweep, Descriptions
|
||||
// See Also: parent(), join_prism(), linear_sweep()
|
||||
// Usage:
|
||||
// prism_connector(desc1, anchor1, desc2, anchor2, [spin_align=]);
|
||||
// Description:
|
||||
// Given descriptions and anchors for two objects, construct a filleted prism that connects the
|
||||
// anchor points on those objects, with a filleted joint at each end. This is an alternative interface
|
||||
// to {{join_prism()}}, and the arguments which describe the prism are the same. You obtain the
|
||||
// object descriptions using {{parent()}}, which can enable prisms to be constructed between objects
|
||||
// at different levels in the object tree. You can also connect an object with itself, for example to
|
||||
// create a hole through an object, or to create an interior connection through a hole.
|
||||
// If you specify a CENTER anchor for an object then the prism will be aimed at the object's CENTER anchor
|
||||
// and joined at a shifted anchor located on the object's surface.
|
||||
// .
|
||||
// The prism will connect anchor points described by the two descriptions you supply. The supported object
|
||||
// types are prismoids, VNFs, cylinders, spheres, and linear sweeps. For prismoids and VNFs you can use any anchor on a face
|
||||
// or edge anchors that include edge geometry. For spheres you can use any anchor. In the case of cylinders and linear sweeps you can
|
||||
// attach to the flat top or bottom in any case, but for side attachments, the shape must not have scaling (so it cannot
|
||||
// be conical) and it must not have any shift. Only right angle cylinders and extrusions are supported.
|
||||
// Anchors on the top and bottom edges are also not supported. When connecting to an extrusion the selected anchor
|
||||
// point must lie on the surface of the shape. This may requires setting `atype="intersect"` when creating the extrusion.
|
||||
// Because of how {{join_prism()}} works, the prism will always make a joint to the shape, but it may be in the wrong location
|
||||
// when the anchor point is not on the surface, something that may be particularly puzzling with CENTER anchors.
|
||||
// .
|
||||
// If you want to shift the prism away from the anchor point you can do that using the `shift1` and `shift2` paramters.
|
||||
// For anchoring to a flat face, the shift is a 2-vector where the y direction corresponds to the direction of the anchor's spin.
|
||||
// For a cylinder or extrusion the shift must be a scalar and shifts along the axis. For sphere shift is not permitted.
|
||||
// .
|
||||
// You can rotate the prism by applying {{zrot()}} to your profile, but the `spin_align` option will enable you to rotate it
|
||||
// relative to the spin directions of the two descriptions you supply. If you set `spin_align=1` then the Y direction of the
|
||||
// profile will align with the spin direction on object 1. If you set `spin_align=2` then it will align with the spin direction on object 2.
|
||||
// You can also set `spin_align` to either 12 or 21 to get an average value between the spins of the two shapes. The 12 and 21 options
|
||||
// produce the same result except when the spins are exactly 180 degrees apart. The default is to align the spin with object 1.
|
||||
// .
|
||||
// When you connect to a flat surface, the prism may extend beyond the edge of the surface if it doesn't fit, and the same thing happens if
|
||||
// a connector runs off either end of a cylinder. But if you connect to a sphere the prism must fully intersect it and if you connect to the curved side
|
||||
// of a cylinder or extrusion the prism must fully intersect the infinite extension of that object. If the prism doesn't intersect
|
||||
// the curved surface in that required fashion, it will not be displayed and you will get an error. You can debug errors
|
||||
// like this by setting `debug_pos=true` which debugs the prism position by displaying an unfilleted prism to help you understand why
|
||||
// your prism did not work. Children are not rendered when `debug_pos=true`.
|
||||
// .
|
||||
// Another failure can occur if your fillet is too large to accomodate the requested fillet size. The fillet is constructed by offsetting every point
|
||||
// in the profile separately and for a large enough fillet size, concave profiles will cross each other, resulting in an invalid self-intersecting fillet.
|
||||
// Normally {{join_prism()}} will issue an error in this situation. The `debug` parameter is passed through to {{join_prism()}} and
|
||||
// tells that module to display invalid self-intersecting geometry to help you understand the problem.
|
||||
// .
|
||||
// When connecting to an edge, artifacts may occur at the corners where the prism doesn't meet the object in the ideal fashion.
|
||||
// Adjsting the points on your prism profile so that a point falls close to the corner will achieve the best result, and make sure
|
||||
// that `smooth_normals` is disabled (the default for edges) because it results in a completely incorrect fillet in this case.
|
||||
// If you connect to an extrusion object, the default value for `smooth_normals` is true, which generally works better when
|
||||
// for a uniformly sampled smooth object, but if your object has corners you may get better results by setting `smooth_normals=false`.
|
||||
// Arguments:
|
||||
// profile = path giving cross section to extrude to create the connecting prism
|
||||
// desc1 = description of first object to connect
|
||||
// anchor1 = connection on point first object
|
||||
// desc2 = description of second object to connect
|
||||
// anchor2 = connection point on second object
|
||||
// ---
|
||||
// shift1 = shift connection point on object1, a scalar for cylinders, extrusions, or edges, a 2-vector for faces, not permitted for spheres
|
||||
// shift2 = shift connection point on object2, a scalar for cylinders, extrusions, or edges, a 2-vector for faces, not permitted for spheres
|
||||
// spin_align = align the spin of the connecting prism to specified object (1 or 2) or if you give 12 or 21, the average of the two spins. Default: 1
|
||||
// scale = scale the profile by this factor at anchor2. Default: 1
|
||||
// n = number of facets to use for the fillets. Default: 15
|
||||
// n1 = number of facets at object1
|
||||
// n2 = number of facets at object2
|
||||
// k = fillet curvature parameter for both ends. Default: 0.7
|
||||
// k1 = fillet curvature parameter at object1
|
||||
// k2 = fillet curvature parameter at object2
|
||||
// uniform = set to false to get non-uniform filleting at both ends. Default: true
|
||||
// uniform1 = set to false for non-uniform filleting at object1
|
||||
// uniform2 = set to false for non-uniform filleting at object2
|
||||
// overlap = amount of overlap of the prism fillet into both objects. Default: 1
|
||||
// overlap1 = amount of overlap of the prism fillet into object1
|
||||
// overlap2 = amount of overlap of the prism fillet into object2
|
||||
// smooth_normals = controls whether normals are smoothed when the object is a prism or edge; no effect otherwise. Default: false if object is an edge, true otherwise
|
||||
// smooth_normals1 = controls whether normals are smoothed when the object1 is a prism or edge; no effect otherwise.
|
||||
// smooth_normals2 = controls whether normals are smoothed when the object2 is a prism or edge; no effect otherwise.
|
||||
// debug = pass-through to the {{join_prism()}} debug parameter. If true then various cases where the fillet self intersects will be displayed instead of creating an error. Default: false
|
||||
// debug_pos = if set to true display an unfilleted prism instead of invoking {{join_prism()}} so that you can diagnose errors about the prism not intersecting the object. Default: false
|
||||
// Named Anchors:
|
||||
// "root" = Root point of the connector prism at the desc1 end, pointing out in the direction of the prism axis (anchor inherited from {{join_prism()}}
|
||||
// "end" = Root point of the connector prism at the desc2 end, pointing out in the direction of the prism axis (anchor inherited from {{join_prism()}}
|
||||
// Example: A circular prism connects a prismoid to a sphere. Note different fillet sizes at each length.
|
||||
// circ = circle(r=3, $fn=48);
|
||||
// prismoid(20,13,shift=[-2,1],h=15) let(prism=parent())
|
||||
// right(30) zrot(20) yrot(12) spheroid(r=10,circum=true,$fn=48) let(ball=parent())
|
||||
// prism_connector(circ,prism,RIGHT,ball,LEFT,fillet1=4,fillet2=1);
|
||||
// Example: Here we attach a rounded triangular prism to a prismoid on the left and a regular prism (vnf geometry type) on the right. Note that the point of the triangle which is on the Y axis is aligned with the spin direction on the prismoid, which is the first object.
|
||||
// $fn=32;
|
||||
// tri = subdivide_path(round_corners([[-3,-2],[0,5],[3,-2]], cut=1), n=32);
|
||||
// prismoid(20,15,h=19) let(p1=parent())
|
||||
// back(15)right(33)zrot(62)xrot(37)zrot(0) regular_prism(n=5, h=30, side=13) let(p2=parent())
|
||||
// prism_connector(tri, p1, RIGHT, p2, FACE(2), fillet=3);
|
||||
// Example: Here is the same example with `spin_align=2` which aligns the connecting prism on the second object
|
||||
// $fn=32;
|
||||
// tri = subdivide_path(round_corners([[-3,-2],[0,5],[3,-2]], cut=1), n=32);
|
||||
// prismoid(20,15,h=19) let(p1=parent())
|
||||
// back(15)right(33)zrot(62)xrot(37)zrot(0) regular_prism(n=5, h=30, side=13) let(p2=parent())
|
||||
// prism_connector(tri, p1, RIGHT, p2, FACE(2), fillet=3, spin_align=2);
|
||||
// Example: Here the connector prism is aligned midway between the spins on the two described objects using `spin_align=12`.
|
||||
// $fn=32;
|
||||
// tri = subdivide_path(round_corners([[-3,-2],[0,5],[3,-2]], cut=1), n=32);
|
||||
// prismoid(20,15,h=19) let(p1=parent())
|
||||
// back(15)right(33)zrot(62)xrot(37)zrot(0) regular_prism(n=5, h=30, side=13) let(p2=parent())
|
||||
// prism_connector(tri, p1, RIGHT, p2, FACE(2), fillet=3, spin_align=12);
|
||||
// Example: Here we apply a shift on object 1. Since this object has a planar connection surface the shift is a 2-vector. Note that the prism has shifted a little too far and is poking out of the connecting cube. When connecting to a planar surface there is no constraint on the extent of the joined prism. It may be much larger than the object it connects to. Note also that the connection on the sphere has shifted to accomodate the change in direction of the prism. If you shift it just a little bit farther forward (perhaps to fit onto a larger cube) the connection to the sphere will fail because the prism doesn't fully intersect the sphere.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid(25) let(cube=parent())
|
||||
// right(40) spheroid(r=15, circum=true,$fn=32) let(ball=parent()){
|
||||
// prism_connector(circ,cube,RIGHT, ball, [-1,0,.4], fillet=2);
|
||||
// %prism_connector(circ,cube,RIGHT, ball, [-1,0,.4], fillet=2,shift1=[-6,0]);
|
||||
// }
|
||||
// Example: In this case because of how the connecting prism is shifted, it does not fully intersect the sphere and you will get an error message stating this. To understand what is happening you can enable the `debug_pos` option which displays an unfilleted prism. You can inspect the result and see that the edge of the prism will not intersect the sphere, especially after a fillet is added.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid(25) let(cube=parent())
|
||||
// right(40) spheroid(r=15, circum=true,$fn=32) let(ball=parent())
|
||||
// prism_connector(circ,cube,RIGHT, ball, [-1,0,.4], fillet=4, shift1=[0,-6],debug_pos=true);
|
||||
// Example: Here two cylinders are connected using a prism shift a shift at each end. Note that the shift is always along the axis of the cylinder. Note that the prisms are a little above the faceted cylinders, exposing a small edge. Using the circum option to enlarge the cylinders will hide this edge inside the cylinders.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// zrot(-20)
|
||||
// ycyl(l=40,d=20) let(x=parent())
|
||||
// right(40) back(9) cyl(l=40,d=20) let(z=parent()){
|
||||
// prism_connector(circ, x, RIGHT, z, LEFT+FWD, fillet=2);
|
||||
// %prism_connector(circ, x, RIGHT, z, LEFT+FWD, fillet=2, shift1=-9, shift2=8);
|
||||
// }
|
||||
// Example: Here the model has an error and attachment point on the cylinder is on the wrong side so the prism passes through the cylinder. The shape you see on the front is the base of the prism connector that would usually be buried inside an object. Later we will see that this can be used for making holes.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// prismoid(20,13,shift=[-2,1],h=15) let(a=parent())
|
||||
// right(30) fwd(9) rot([20,15,17]) cyl(r=10,h=30)
|
||||
// prism_connector(circ,parent(),FWD,a,RIGHT,fillet=2);
|
||||
// Example: Using the CENTER anchor lets you create a connection, especially for spheres and cylinders, that puts the connecting prism in the best spot, without the need to figure out what the right anchor is.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid([18,10,20],anchor=LEFT) let(cube=parent())
|
||||
// move([11,-23,14])
|
||||
// sphere(d=10) let(ball=parent())
|
||||
// prism_connector(circ,cube,CTR,ball,CTR,fillet=2);
|
||||
// Example: You can still apply shifts with CENTER anchors. In this case we shift the two connectors outward so that their fillets don't interfere on the cube. Note that we give shift as a scalar, which is interpreted as shift in just the x direction.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid([30,10,20]) let(cube=parent())
|
||||
// fwd(22)
|
||||
// xcopies(n=2,spacing=45)
|
||||
// cyl(d=10,h=10,circum=true,$fn=64) let(cyl=parent())
|
||||
// prism_connector(circ,cube,CTR,cyl,CTR,fillet1=3,fillet2=2,shift1=2*(2*$idx-1));
|
||||
// Example: Here is a center anchor connection using an extrusion
|
||||
// flower = [for(theta=lerpn(0,360,180,endpoint=false))
|
||||
// (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]];
|
||||
// linear_sweep(flower, height=29,scale=1,atype="intersect")
|
||||
// let(sweep=parent())
|
||||
// move([24,-22,20]) sphere(d=10)
|
||||
// prism_connector(circle(r=2.2,$fn=32), sweep, CTR, parent(),CTR, fillet=2);
|
||||
|
||||
// Example: Connecting to edges. In this example the triangular prism is aligned with object1, the big cube, so its corner is at the edge. You can't align it with both edges at the same time; that would requires twisting the prism.
|
||||
// $fn=32;
|
||||
// tri = subdivide_path(round_corners([[-3,-2],[0,5],[3,-2]], cut=1), maxlen=1,closed=true);
|
||||
// zrot(55)
|
||||
// cuboid(30) let(big=parent())
|
||||
// move([30,-30,-10]) xrot(40) cuboid(20) let(small=parent())
|
||||
// prism_connector(tri, big,RIGHT+FWD, small, BACK+LEFT, fillet=2);
|
||||
// Example: Here is the same example again, but with the spin aligned to object2, the small cube. Note now that the corner is **not** aligned on the edge of the big cube. You can't align it with both edges at the same time; that would requires twisting the prism.
|
||||
// $fn=32;
|
||||
// tri = subdivide_path(round_corners([[-3,-2],[0,5],[3,-2]], cut=1), maxlen=1,closed=true);
|
||||
// zrot(55)
|
||||
// cuboid(30) let(big=parent())
|
||||
// move([30,-30,-10]) xrot(40) cuboid(20) let(small=parent())
|
||||
// prism_connector(tri, big,RIGHT+FWD, small, BACK+LEFT, spin_align=2,fillet=2);
|
||||
// Example: attaching to edges doesn't always produce a good looking result, and sometimes you may get unexpected errors about the fit of the fillet. If you connect a circular prism to an edge you definitely want an even number of points so the top and bottom can line up with the edge. But increasing the point count may make the result appear worse, like this artifact:
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid(20) let(edge=parent())
|
||||
// move([30,-30,-8]) zrot(-45) cuboid(20) let(extra=parent())
|
||||
// prism_connector(circ, edge, RIGHT+FWD, extra, LEFT, fillet=2);
|
||||
// Example(3D,VPR=[80.9,0,55.8],VPT=[11.9865,-12.0228,4.48816],VPD=15.3187): Attaching to edges doesn't always produce a good looking result, and sometimes you may get unexpected errors about the fit of the fillet. If you connect a circular prism to an edge you definitely want an even number of points so the top and bottom can line up with the edge. But you may find that artifacts appear when you increase the point count like in this example below where the prism's joint to the edge has a little groove:
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// cuboid(20) let(edge=parent())
|
||||
// move([30,-30,-8]) zrot(-45) cuboid(20) let(extra=parent())
|
||||
// prism_connector(circ, edge, RIGHT+FWD, extra, LEFT, fillet=2);
|
||||
// Example(3D,VPR=[80.9,0,55.8],VPT=[11.9865,-12.0228,4.48816],VPD=15.3187): This artifact happens because of normals to the prism that cross the edge at a shallow angle, and you can remove it by either decreasing the number of points (32 works in this case) or by stretching out the circle so that the top is flatter. Generally results will be best if you can get a point on the edge and if the top surface is perpendicular to the edge.
|
||||
// circ = xscale(1.2,circle(r=3, $fn=64));
|
||||
// cuboid(20) let(edge=parent())
|
||||
// move([30,-30,-8]) zrot(-45) cuboid(20) let(extra=parent())
|
||||
// prism_connector(circ, edge, RIGHT+FWD, extra, LEFT, fillet=2);
|
||||
// Example(3D,VPR=[80.9,0,55.8],VPT=[11.9865,-12.0228,4.48816],VPD=15.3187): When no point falls on the edge you can get an artifact like this, where the connector prism is underneath the corner.
|
||||
// circ = xscale(1.2,circle(r=3, $fn=31));
|
||||
// cuboid(20) let(edge=parent())
|
||||
// move([30,-30,-8]) zrot(-45) cuboid(20) let(extra=parent())
|
||||
// #prism_connector(circ, edge, RIGHT+FWD, extra, LEFT, fillet=2);
|
||||
// Example: We can attach to the top surface of a shifted cone, but when attaching to the curved surface, only a right angle cylinder is supported.
|
||||
// $fn=32;
|
||||
// flower = scale(.6,[for(theta=lerpn(0,360,90,endpoint=false)) (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]]);
|
||||
// cyl(d1=40, d2=30,h=30, shift=[4,9]) let(cone=parent())
|
||||
// up(40) back(30)xcyl(d=30,l=30,$fn=64,circum=true)
|
||||
// prism_connector(flower, cone, TOP, parent(), FWD+BOT, fillet=2.5);
|
||||
// Example(3D,VPT=[2.33096,4.77324,9.30076],VPR=[85.8,0,358.4],VPD=102.06): This example scales the end of the prism, has different fillets at each end, and uses shifting to adjust its position.
|
||||
// cyl(d=30,h=8) let(bot=parent())
|
||||
// up(20)right(8)xrot(-20)yrot(11)cyl(d=18,h=8) let(top=parent())
|
||||
// prism_connector(circle(d=20,$fn=64), bot, TOP, top, BOT, scale=0.4,
|
||||
// fillet1=2.5, shift1=3,fillet2=2, shift2=[-2,-2.2]);
|
||||
// Example: Here we connect a prism to a linear sweep. (Note that you must use {{linear_sweep()}}, not linear_extrude().)
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// flower = scale(.4,[for(theta=lerpn(0,360,180,endpoint=false)) (15+1.3*sin(6*theta))*[cos(theta),sin(theta)]]);
|
||||
// zrot(-90)
|
||||
// linear_sweep(flower, h=22) let(sweep=parent())
|
||||
// zrot(90)right(40)zrot(15)yrot(12) cuboid(12) let(cube=parent())
|
||||
// prism_connector(circ,sweep,BACK,cube,LEFT,fillet=2);
|
||||
// Example: You can use the same object for `desc1` and `desc2` with different anchors to create a filleted hole. Note that if you don't enlarge overlap from its default value of 1 then parts of the cylinder don't get removed by the difference.
|
||||
// circ = circle(r=8, $fn=64);
|
||||
// back_half()
|
||||
// diff()
|
||||
// cyl(d=40,h=50,$fn=32)
|
||||
// tag("remove") prism_connector(circ,parent(),LEFT,parent(),RIGHT,
|
||||
// shift1=-8,shift2=7,fillet=6,overlap=3);
|
||||
// Example: You can also use interior connectors to bridge across holes as shown in this example. Note also that you can apply operations like rotation to the connector.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// diff()
|
||||
// highlight_this() cyl(d=85,h=39)
|
||||
// tag("remove") cyl(d=75,h=40,$fn=128)
|
||||
// tag("keep") zrot_copies(n=4)
|
||||
// prism_connector(circ,parent(),[-1,.2],parent(),[1,.4],shift1=12,shift2=-12,fillet=2);
|
||||
// Example(3D,Med): Here we use the {{zrot_copies()}} distributor to create copies of objects and create a connector to a non-symmetrically placed object. All all the connectors are different because we change the anchor point that goes with the second description.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// right(4)up(25)xrot(15) cyl(r=20,h=30,circum=true,$fn=64) let(cyl=parent())
|
||||
// restore()
|
||||
// zrot_copies(n=5) right(40)zrot(45)cuboid(18)
|
||||
// prism_connector(circ, parent(), TOP, cyl, [cos(360/5*$idx), sin(360/5*$idx), 0], fillet1=3,fillet2=7);
|
||||
// Example(3D,Med): In the previous example we used a distributor to create copies of an object and build connectors from those copies to a different object. What if you want to create connectors between copies created by a distributor? One powerful way to do this is to create an array of descriptions and use that array to make the connectors. It's convenient to put your object into a module so you don't have to repeat it, but make sure that your module takes children, or the connectors won't run! Here we create the objects first, and then we separately create the connectors as a child of a single hidden instance of the object. That second construction is needed so we can get the description of the object, but we don't want it to show up in the model.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// module object() cuboid(18)children();
|
||||
// T_list = arc_copies(rx=80,ry=60,n=5,sa=0,ea=180);
|
||||
// for(T=T_list) multmatrix(T) object();
|
||||
// hide_this()object()
|
||||
// let(desc = transform_desc(T_list,parent()))
|
||||
// for(d=pair(desc))
|
||||
// prism_connector(circ, d[0], BACK, d[1], FWD, fillet=5);
|
||||
// Example(3D,Med): We can change the object in the above example to vary between cube and cylinder.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// T_list = arc_copies(rx=80,ry=60,n=5,sa=0,ea=180);
|
||||
// module object(ind)
|
||||
// if (ind%2==0) cuboid(18)children();
|
||||
// else cyl(d=30,h=18,circum=true) children();
|
||||
// for(i=idx(T_list)) multmatrix(T_list[i]) object(i);
|
||||
// hide_this() object(0) let(even=parent())
|
||||
// hide_this() object(1) let(obj=[even,parent()], p=pair(T_list))
|
||||
// for(i=[0:len(T_list)-2])
|
||||
// prism_connector(circ, transform_desc(T_list[i],select(obj,i)),BACK,
|
||||
// transform_desc(T_list[i+1],select(obj,i+1)), FWD,
|
||||
// fillet=4);
|
||||
// Example(3D,Med): Another way to establish connections between objects is with {{desc_copies()}} which provides functions to access the descriptions of the other objects in the set. Note that in OpenSCAD 2021.01 you cannot call `$prev()` and `$next()` directly. In development versions you can call them directly and hence the example could be slightly simplified.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// desc_copies(arc_copies(rx=80,ry=60,n=7,sa=0,ea=360))
|
||||
// spheroid(11,circum=true) let(next=$next,prev=$prev)
|
||||
// prism_connector(circ, prev(),BACK+LEFT, next(), FWD+LEFT, fillet=5, debug_pos=false);
|
||||
// Example(3D,Med): Using CENTER anchors can make a construction like this much easier. In this example the anchors need to shift around from the pointy end to the flat end of the ellipse, which would be annoying to calculate by hand.
|
||||
// desc_copies(arc_copies(rx=85,ry=45,n=12))
|
||||
// cyl(d=15,h=27,circum=true,rounding=5,$fn=64)
|
||||
// prism_connector(circle(r=3,$fn=32), parent(), CTR, $next(), CTR, fillet=4);
|
||||
|
||||
// Example(3D,Med): When using {{desc_copies()}} with a varying shape you have to conditionally show only the correct shape for each index, but still specify all the shapes so you can collect their descriptions.
|
||||
// circ = circle(r=3, $fn=64);
|
||||
// desc_copies(arc_copies(rx=60,ry=80,n=5,sa=-20,ea=200))
|
||||
// hide($idx%2==0?"cyl":"cube")
|
||||
// tag_this("cyl")cyl(d=30,h=30) let(cyl=parent())
|
||||
// tag_this("cube")cuboid([22,22,30])
|
||||
// let(
|
||||
// obj=[parent(),cyl],
|
||||
// next=$next,
|
||||
// shift=$idx%2==0?[0,6]:-6
|
||||
// )
|
||||
// if($idx<$count-2)
|
||||
// prism_connector(scale(.8,circ),
|
||||
// select(obj,$idx),BACK,
|
||||
// next(2,select(obj,$idx+2)), FWD, fillet=4,shift1=shift,debug_pos=false);
|
||||
|
||||
|
||||
|
||||
// Get the object type from the specified geometry and anchor point
|
||||
|
||||
// Note that profile is needed just to find its dimensions for making a big enough edge profile
|
||||
function _get_obj_type(ind,geom,anchor,prof) =
|
||||
geom[0]=="spheroid" ? "sphere"
|
||||
: geom[0]=="conoid" ? let(
|
||||
axis = geom[5],
|
||||
anchor = rot(from=axis, to=UP, p=anchor)
|
||||
)
|
||||
anchor==UP || anchor==DOWN ? "plane"
|
||||
: assert(geom[1]==geom[2], str("For anchors other than TOP/BOTTOM, cylinder from desc",ind," must be non-conical, with same size at each end"))
|
||||
assert(geom[4]==[0,0], str("For anchors other than TOP/BOTTOM, cylinder from desc",ind," must be a right-angle cylinder with zero shift"))
|
||||
assert(anchor.z==0,str("Anchor for cylinder for desc",ind," is on the cylinder's edge. This is not supported."))
|
||||
"cyl"
|
||||
: geom[0]=="prismoid" || geom[0]=="vnf_extent" ?
|
||||
assert(geom[0]!="prismoid" || sum(v_abs(anchor))<3, "Cannot give a corner anchor for prismoid geometry")
|
||||
let(
|
||||
anch = _find_anchor(anchor, geom),
|
||||
edge_angle = len(anch)==5 ? struct_val(anch[4],"edge_angle") : undef
|
||||
)
|
||||
is_undef(edge_angle)
|
||||
? "plane"
|
||||
: let(
|
||||
y = 20*max(v_abs(full_flatten(prof))),
|
||||
x = y/tan(edge_angle/2)
|
||||
)
|
||||
[[x,-y],[0,0], [x,y]]
|
||||
: starts_with(geom[0], "extrusion") ?
|
||||
anchor==UP || anchor==DOWN ? "plane"
|
||||
:
|
||||
assert(geom[3]==0, str("Extrusion in desc", ind, " has nonzero twist, which is not supported."))
|
||||
assert(geom[5]==[0,0], str("Extrusion in desc", ind, " has nonzero shift, which is not supported."))
|
||||
assert(geom[4]==[1,1], str("Extrusion in desc",ind, " is conical, which is not supported."))
|
||||
assert(anchor.z==0,str("Anchor for extrusion for desc",ind," is on the extrusions top/bottom edge. This is not supported."))
|
||||
let(reg = region_parts(geom[1]))
|
||||
assert(len(reg)==1, "Region has multiple disconnected components, which is not supported")
|
||||
let( // Here we shift the region so that the anchor point is at the origin
|
||||
anch = _find_anchor(anchor, geom)
|
||||
)
|
||||
rot(from=anch[2],to=LEFT, p=move(-anch[1], reg[0][0]))
|
||||
: assert(false, str("Unsupported geometry:", geom[0]));
|
||||
|
||||
|
||||
/// Check and compute the shift parameter for different object types
|
||||
/// Arguments
|
||||
/// ind = object index for error messages, either 1 or 2
|
||||
/// type = object type
|
||||
/// shift = given shift parameter
|
||||
|
||||
function _check_join_shift(ind,type,shift,flip) =
|
||||
type=="sphere" ? assert(shift==0, str("Cannot give a (nonzero) shift",ind," for joining to a spherical object")) [0,0,0]
|
||||
: type=="cyl" ? assert(is_finite(shift), str("Value shift",ind," for cylinder object must be a scalar")) shift*RIGHT
|
||||
: is_list(type) ? assert(is_finite(shift), str("Value shift",ind," for an edge must be a scalar")) shift*RIGHT
|
||||
: /*type==plane*/ assert(is_finite(shift) || is_vector(shift,2), str("Value for shift",ind," for planar face of object must be a scalar or 2-vector"))
|
||||
is_list(shift)? flip ? [shift.y,-shift.x]: shift
|
||||
: flip ? [0,-shift] : [shift,0];
|
||||
|
||||
|
||||
function _is_geom_an_edge(geom,anchor) =
|
||||
(geom[0]=="prismoid" || geom[0]=="vnf_extent")
|
||||
&& (
|
||||
let(anch = _find_anchor(anchor, geom))
|
||||
is_def(struct_val(anch[4], "edge_angle"))
|
||||
);
|
||||
|
||||
|
||||
|
||||
function _prismoid_isect(geom, line, bounded, flip=false) =
|
||||
let(
|
||||
size = [for (c = geom[1]) max(0,c)],
|
||||
size2 = [for (c = geom[2]) max(0,c)],
|
||||
shift=point2d(geom[3]),
|
||||
axis=point3d(geom[4]),
|
||||
h=size.z,
|
||||
bot=path3d(rect(point2d(size)),-h/2),
|
||||
top=path3d(move(shift, rect(size2)),h/2),
|
||||
modline = rot(from=axis,to=UP, p=line),
|
||||
isect = [ polygon_line_intersection(top, modline, bounded),
|
||||
polygon_line_intersection(bot, modline, bounded),
|
||||
for(i=[0:3]) polygon_line_intersection([top[i], bot[i], select(bot,i+1),select(top,i+1)], modline, bounded)
|
||||
],
|
||||
faceanch = [TOP, BOT, FWD, LEFT, BACK, RIGHT],
|
||||
hits = [for(i=idx(isect)) if (isect[i]) [faceanch[i], isect[i]]],
|
||||
check = assert(len(hits)>0, "Line does not intersect the prismoid."),
|
||||
anchor = rot(from=UP,to=axis,p=sum(column(hits,0))),
|
||||
anchlen = sum(v_abs(anchor)),
|
||||
ipt = hits[0][1],
|
||||
anch = _find_anchor(anchor, geom),
|
||||
anchpt = anch[1],
|
||||
myshift = anchlen==3 ? 0
|
||||
: let(
|
||||
z = anch[2],
|
||||
y = rot(from=UP,to=z, p=zrot(anch[3], BACK)),
|
||||
x = cross(y,z)
|
||||
)
|
||||
anchlen==2 ? (ipt-anchpt) * y * RIGHT
|
||||
: (!flip?ident(2):[[0,1],[-1,0]])*[x,y]*(ipt-anchpt)
|
||||
)
|
||||
[anchor, myshift];
|
||||
|
||||
// Find intersection with tops of a cone or if those don't intersect,
|
||||
// then the sides of a right angle cylinder only.
|
||||
function _cone_isect(geom,line,bounded,flip) =
|
||||
let(
|
||||
rr1=geom[1],
|
||||
rr2=geom[2],
|
||||
r1 = is_num(rr1)? [rr1,rr1] : point2d(rr1),
|
||||
r2 = is_num(rr2)? [rr2,rr2] : point2d(rr2),
|
||||
r=[r1,r2],
|
||||
length=geom[3],
|
||||
shift=point2d(geom[4]),
|
||||
axis=point3d(geom[5]),
|
||||
modline = rot(from=axis,to=UP, p=line),
|
||||
|
||||
btisect = [for(dir=[-1,1]) plane_line_intersection(plane_from_normal(UP,dir*length/2*UP), modline, RAY)],
|
||||
tbhit = [for(i=[0:1])
|
||||
if (is_def(btisect[i]) && (btisect[i].x-shift.x)^2/r[i].x^2+(btisect[i].y-shift.y)^2/r[i].y^2<=1) i ],
|
||||
tbresult = len(tbhit)==0 ? undef
|
||||
: let(
|
||||
anchor = rot(from=UP,to=axis,p=[0,0,2*tbhit[0]-1]),
|
||||
anch = _find_anchor(anchor,geom),
|
||||
z = anch[2],
|
||||
y = rot(from=UP,to=z, p=zrot(anch[3], BACK)),
|
||||
x = cross(y,z),
|
||||
shift = (!flip?ident(2):[[0,1],[-1,0]])*[x,y]*(rot(from=UP,to=axis,p=btisect[tbhit[0]])-anch[1])
|
||||
)
|
||||
[anchor,shift]
|
||||
)
|
||||
is_def(tbresult) ? tbresult
|
||||
:
|
||||
assert(r1==r2 && r1[0]==r2[0] && shift==[0,0], "Center anchor intersects curved side of cone or shifted cylinder, which is not allowed")
|
||||
let(
|
||||
ray = modline[1]-modline[0],
|
||||
anchor = rot(from=UP,to=axis,p=point3d(unit(point2d(ray)))),
|
||||
slope = ray.z/norm([ray.x,ray.y]),
|
||||
anch = _find_anchor(anchor,geom),
|
||||
z = anch[2],
|
||||
y = rot(from=UP,to=z,p=zrot(anch[3], BACK)),
|
||||
shift = (r1[0]*slope)*(axis==UP?1:(cross(y,z)*axis))
|
||||
)
|
||||
[anchor,shift*RIGHT];
|
||||
|
||||
|
||||
|
||||
function _extrusion_isect(geom,line,bounded,flip) =
|
||||
let(
|
||||
region=geom[1],
|
||||
length=geom[2],
|
||||
twist = geom[3],
|
||||
scale=point2d(geom[4]),
|
||||
shift=point2d(geom[5]),
|
||||
|
||||
reg=region_parts(region),
|
||||
check1 = assert(len(reg)==1, "Region has multiple disconnected components, which is not supported"),
|
||||
path = reg[0][0],
|
||||
|
||||
bot_top = [path3d(path, -length/2),
|
||||
move(shift,zrot(twist,scale(scale,path3d(path, length/2))))],
|
||||
|
||||
btisect = [for(poly=bot_top) polygon_line_intersection(poly, line, bounded)],
|
||||
tbhit = [for(i=[0:1]) if (is_vector(btisect[i])) i],
|
||||
|
||||
tbresult = len(tbhit)==0 ? undef
|
||||
:
|
||||
let(
|
||||
anchor = [0,0,2*tbhit[0]-1],
|
||||
anch = _find_anchor(anchor,geom),
|
||||
z = anch[2],
|
||||
y = rot(from=UP,to=z, p=zrot(anch[3], BACK)),
|
||||
x = cross(y,z),
|
||||
shift = (!flip?ident(2):[[0,1],[-1,0]])*[x,y]*(btisect[tbhit[0]]-anch[1])
|
||||
)
|
||||
[anchor,shift]
|
||||
)
|
||||
is_def(tbresult) ? tbresult
|
||||
:
|
||||
assert(twist==0, "Extrusion has nonzero twist which is not supported")
|
||||
assert(shift==[0,0], "Extrusion has nonzero shift, which is not supported.")
|
||||
assert(scale==[1,1], "Extrusion is conical, which is not supposrted")
|
||||
let(
|
||||
isect = polygon_line_intersection(path, path2d(line), RAY),
|
||||
check1=assert(is_def(isect), "Cannot find side anchor to extrusion"),
|
||||
|
||||
pt = let(
|
||||
pts = flatten(isect),
|
||||
dists = [for(pt=pts) norm(pt-line[0])]
|
||||
)
|
||||
pts[max_index(dists)],
|
||||
ray = line[1]-line[0],
|
||||
anchor = point3d(unit(point2d(ray))),
|
||||
slope = ray.z/norm([ray.x,ray.y]),
|
||||
anch = _find_anchor(anchor,geom),
|
||||
z = anch[2],
|
||||
y = rot(from=UP,to=z,p=zrot(anch[3], BACK)),
|
||||
shift = (norm(pt)*slope)
|
||||
)
|
||||
[anchor,shift*RIGHT];
|
||||
|
||||
|
||||
function _find_center_anchor(desc1, desc2, anchor2, flip) =
|
||||
let(
|
||||
pt2 = desc_point(desc2, anchor=anchor2),
|
||||
line = [CTR,desc_attach(desc1,CTR,p=pt2,reverse=true)],
|
||||
geom = desc1[1]
|
||||
)
|
||||
geom[0]=="prismoid" ? _prismoid_isect(geom, line, RAY, flip)
|
||||
: geom[0]=="conoid" ? _cone_isect(geom,line,RAY,flip)
|
||||
: geom[0]=="spheroid" ? [unit(line[1]-line[0]), [0,0,0]]
|
||||
: starts_with(geom[0],"extrusion") ? _extrusion_isect(geom,line,RAY,flip)
|
||||
: assert(false,str("Center anchor not supported with geometry type ",geom[0]));
|
||||
|
||||
|
||||
|
||||
|
||||
module prism_connector(profile, desc1, anchor1, desc2, anchor2, shift1=0, shift2=0, spin_align=1,
|
||||
scale=1,
|
||||
fillet, fillet1, fillet2,
|
||||
overlap, overlap1, overlap2,
|
||||
k, k1, k2, n, n1, n2,
|
||||
uniform, uniform1, uniform2,
|
||||
smooth_normals, smooth_normals1, smooth_normals2,
|
||||
debug=false, debug_pos=false)
|
||||
{
|
||||
base_fillet = default(fillet1,fillet);
|
||||
aux_fillet = default(fillet2,fillet);
|
||||
|
||||
base_overlap = first_defined([overlap1,overlap,1]);
|
||||
aux_overlap = first_defined([overlap2,overlap,1]);
|
||||
|
||||
base_n = first_defined([n1,n,15]);
|
||||
aux_n = first_defined([n2,n,15]);
|
||||
|
||||
base_uniform = first_defined([uniform1, uniform, true]);
|
||||
aux_uniform = first_defined([uniform2, uniform, true]);
|
||||
|
||||
base_k = first_defined([k1,k,0.7]);
|
||||
aux_k = first_defined([k2,k,0.7]);
|
||||
|
||||
profile = force_path(profile,"profile");
|
||||
dummy0 = assert(is_path(profile,2), "profile must be a 2d path");
|
||||
|
||||
corrected_base_anchor = is_vector(anchor1) && norm(anchor1)==0 ? _find_center_anchor(desc1,desc2,anchor2,true) : undef;
|
||||
corrected_aux_anchor = is_vector(anchor2) && norm(anchor2)==0 ? _find_center_anchor(desc2,desc1,anchor1,false) : undef;
|
||||
|
||||
|
||||
base_anchor=is_string(anchor1) ? anchor1
|
||||
: is_def(corrected_base_anchor) ? corrected_base_anchor[0]
|
||||
: point3d(anchor1);
|
||||
aux_anchor=is_string(anchor2) ? anchor2
|
||||
: is_def(corrected_aux_anchor) ? corrected_aux_anchor[0]
|
||||
: point3d(anchor2);
|
||||
|
||||
base=desc1;
|
||||
aux=desc2;
|
||||
|
||||
current = parent();
|
||||
tobase = current==base ? ident(4) : linear_solve(current[0],base[0]); // Maps from current frame into the base frame
|
||||
auxmap = linear_solve(base[0], aux[0]); // Map from the base (desc1) coordinate frame into the aux (desc2) coordinate frame
|
||||
|
||||
dummy = assert(is_vector(base_anchor) || is_string(base_anchor), "anchor1 must be a string or a 3-vector")
|
||||
assert(is_vector(aux_anchor) || is_string(aux_anchor), "anchor2 must be a string or a 3-vector")
|
||||
assert(is_rotation(auxmap), "desc1 and desc2 are not related to each other by a rotation (and translation)");
|
||||
|
||||
base_type = _get_obj_type(1,base[1],base_anchor,profile);
|
||||
base_axis = base_type=="cyl" ? base[1][5] : RIGHT;
|
||||
base_edge = _is_geom_an_edge(base[1],base_anchor);
|
||||
base_r = in_list(base_type,["cyl","sphere"]) ? base[1][1] : 1;
|
||||
base_anch = _find_anchor(base_anchor, base[1]);
|
||||
base_spin = base_anch[3];
|
||||
base_anch_pos = base_anch[1];
|
||||
base_anch_dir = base_anch[2];
|
||||
|
||||
prelim_shift1 = _check_join_shift(1,base_type,shift1,true);
|
||||
shift1 = corrected_base_anchor ? corrected_base_anchor[1] + prelim_shift1 : prelim_shift1;
|
||||
aux_type = _get_obj_type(2,aux[1],aux_anchor,profile);
|
||||
aux_anch = _find_anchor(aux_anchor, aux[1]);
|
||||
aux_edge = _is_geom_an_edge(aux[1],aux_anchor);
|
||||
aux_r = in_list(aux_type,["cyl","sphere"]) ? aux[1][1] : 1;
|
||||
aux_anch_pos = aux_anch[1];
|
||||
aux_anch_dir = aux_anch[2];
|
||||
aux_spin = aux_anch[3];
|
||||
aux_spin_dir = apply(rot(from=UP,to=aux_anch[2])*zrot(aux_spin),BACK);
|
||||
aux_axis = aux_type=="cyl" ? aux[1][5] : RIGHT;
|
||||
prelim_shift2 = _check_join_shift(2,aux_type,shift2,false);
|
||||
shift2 = corrected_aux_anchor ? corrected_aux_anchor[1] + prelim_shift2 : prelim_shift2;
|
||||
|
||||
|
||||
base_smooth_normals = first_defined([smooth_normals1, smooth_normals,!base_edge]);
|
||||
aux_smooth_normals = first_defined([smooth_normals2, smooth_normals,!aux_edge]);
|
||||
|
||||
backdir = base_type=="cyl" ? base_axis
|
||||
: apply(rot(from=UP,to=base_anch_dir)*zrot(base_spin),BACK);
|
||||
anch_shift = base_type=="plane" || is_list(base_type) ? base_anch_pos : CENTER;
|
||||
|
||||
|
||||
// Map from the starting position for a join_prism object to
|
||||
// the standard position for the object.
|
||||
// If the aux object is an edge (type is a list) then the starting position
|
||||
// of the prism is with the edge lying on the X axis and the object below.
|
||||
aux_to_canonical = aux_type=="sphere" ? IDENT
|
||||
: aux_type=="cyl" ? frame_map(x=aux_axis, z=aux_anch[2])
|
||||
: aux_type=="plane" ? move(aux_anch_pos) * rot(from=UP, to=aux_anch[2])*zrot(aux_spin)
|
||||
: /* list */ move(aux_anch_pos) * frame_map(z=aux_anch[2],x=aux_spin_dir) ;
|
||||
|
||||
// aux_T is the map that maps the auxiliary object from its initial position to
|
||||
// the position for the prism. The initial position is centered for a sphere,
|
||||
// with the axis X aligned for a cylinder, and with the face of a polyhedron
|
||||
// laying in the XY plane for polyhedra.
|
||||
aux_T = move(-shift1)
|
||||
* frame_map(x=backdir, z=base_anch_dir, reverse=true)
|
||||
* move(-anch_shift)
|
||||
* auxmap
|
||||
* aux_to_canonical
|
||||
* move(shift2);
|
||||
aux_root = aux_type=="plane" || is_list(aux_type) || aux_anchor==CTR ? apply(aux_T,CTR)
|
||||
: apply(aux_T * matrix_inverse(aux_to_canonical), aux_anch_pos);
|
||||
|
||||
base_root = base_type=="plane" || is_list(base_type) || base_anchor==CTR ? CENTER : base_r*UP;
|
||||
|
||||
prism_axis = aux_root-base_root;
|
||||
|
||||
base_inside = prism_axis.z<0 ? -1 : 1;
|
||||
|
||||
aux_normal = aux_type=="cyl" || aux_type=="sphere" ? apply(aux_T*matrix_inverse(aux_to_canonical), aux_anch[2]) - apply(aux_T*matrix_inverse(aux_to_canonical), CTR)
|
||||
: apply(aux_T, UP) - apply(aux_T,CTR); // Is this right? Added second term
|
||||
aux_inside = aux_normal*(base_root-aux_root) < 0 ? -1 : 1;
|
||||
|
||||
shaft = rot(from=UP,to=prism_axis, p=zrot(base_spin,BACK));
|
||||
|
||||
obj1_back = apply(frame_map(x=backdir,z=base_anch_dir,reverse=true)*rot(from=UP,to=base_anch_dir)*zrot(base_spin),BACK);
|
||||
obj2_back = aux_type=="plane" ? apply(aux_T,BACK)-apply(aux_T,CTR)
|
||||
: is_list(aux_type) ? apply(aux_T*matrix_inverse(frame_map(z=aux_anch[2],x=aux_spin_dir)),aux_spin_dir)-apply(aux_T,CTR)
|
||||
: aux_type=="sphere"? apply(aux_T,aux_spin_dir)-apply(aux_T,CTR)
|
||||
/*cyl*/ : apply(aux_T*matrix_inverse(aux_to_canonical),aux_spin_dir)-apply(aux_T,CTR);
|
||||
|
||||
v1 = vector_perp(prism_axis, shaft);
|
||||
v2 = vector_perp(prism_axis, obj1_back);
|
||||
v3 = vector_perp(prism_axis, obj2_back);
|
||||
sign1 = cross(v1,v2)*prism_axis < 0 ? 1 : -1;
|
||||
sign2 = cross(v3,v1)*prism_axis < 0 ? 1 : -1;
|
||||
|
||||
spin1 = sign1 * vector_angle(v1,v2);
|
||||
spin2 = -sign2 * vector_angle(v3,v1);
|
||||
spin = spin_align==1 ? spin1
|
||||
: spin_align==2 ? spin2
|
||||
: spin_align==12 ? mean_angle(spin1,spin2)
|
||||
: spin_align==21 ? mean_angle(spin2,spin1)
|
||||
: assert(false, str("spin_align must be one of 1, 2, 12, or 21 but was ",spin_align));
|
||||
multmatrix(tobase)
|
||||
move(anch_shift)
|
||||
frame_map(x=backdir, z=base_anch_dir)
|
||||
move(shift1){
|
||||
// For debugging spin, shows line in the spin direction
|
||||
//stroke([aux_root,aux_root+unit(obj2_back)*15], width=1,color="lightblue");
|
||||
//stroke([base_root,base_root+unit(obj1_back)*15], width=1,color="lightgreen");
|
||||
|
||||
if (debug_pos)
|
||||
move(base_root)rot(from=UP,to=prism_axis)
|
||||
linear_extrude(height=norm(base_root-aux_root))zrot(base_spin-spin)polygon(profile);
|
||||
else{
|
||||
join_prism(zrot(base_spin-spin,profile),
|
||||
base=base_type, base_r=u_mul(base_r,base_inside),
|
||||
aux=aux_type, aux_T=aux_T, aux_r=u_mul(aux_r,aux_inside),
|
||||
scale=scale,
|
||||
start=base_root, end=aux_root,
|
||||
base_k=base_k, aux_k=aux_k, base_overlap=base_overlap, aux_overlap=aux_overlap,
|
||||
base_n=base_n, aux_n=aux_n, base_fillet=base_fillet, aux_fillet=aux_fillet,
|
||||
base_smooth_normals = base_smooth_normals, aux_smooth_normals=aux_smooth_normals,
|
||||
debug=debug,
|
||||
_name1="desc1", _name2="desc2") children();
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
// vim: expandtab tabstop=4 shiftwidth=4 softtabstop=4 nowrap
|
||||
|
||||
@@ -1817,7 +1817,7 @@ module spiral_sweep(poly, h, r, turns=1, taper, r1, r2, d, d1, d2, internal=fals
|
||||
// path_sweep(shape,path,method="natural"){
|
||||
// attach(["start","end"]) anchor_arrow(s=5);
|
||||
// }
|
||||
// Example(Med,NoScales,VPR=[78.1,0,43.2],VPT=[2.18042,-0.485127,1.90371],VPD=74.4017): The "start" and "end" anchors are located at the origin point of the swept shape.
|
||||
// Example(Med,NoScales,VPR=[78.1,0,43.2],VPT=[2.18042,-0.485127,1.90371],VPD=74.4017): The "start-centroid" and "end-centroid" anchors are located at the centroid the swept shape.
|
||||
// shape = back_half(right_half(star(n=5,id=5,od=10)),y=-1);
|
||||
// path = arc(angle=[0,180],d=30);
|
||||
// path_sweep(shape,path,method="natural"){
|
||||
|
||||
@@ -29,14 +29,15 @@
|
||||
// base = Height of slider base.
|
||||
// wall = Width of wall behind each side of the slider.
|
||||
// ang = Overhang angle for slider, to facilitate supportless printig.
|
||||
// chamfer = Size of chamfer. Default: 2.
|
||||
// anchor = Translate so anchor point is at origin (0,0,0). See [anchor](attachments.scad#subsection-anchor). Default: `CENTER`
|
||||
// spin = Rotate this many degrees around the Z axis after anchor. See [spin](attachments.scad#subsection-spin). Default: `0`
|
||||
// orient = Vector to rotate top towards, after spin. See [orient](attachments.scad#subsection-orient). Default: `UP`
|
||||
// $slop = The printer-specific slop value to make parts fit just right.
|
||||
// Example:
|
||||
// slider(l=30, base=10, wall=4, $slop=0.2, spin=90);
|
||||
function slider(l=30, w=10, h=10, base=10, wall=5, ang=30, anchor=BOTTOM, spin=0, orient=UP) = no_function("slider");
|
||||
module slider(l=30, w=10, h=10, base=10, wall=5, ang=30, anchor=BOTTOM, spin=0, orient=UP)
|
||||
function slider(l=30, w=10, h=10, base=10, wall=5, ang=30, chamfer=2, anchor=BOTTOM, spin=0, orient=UP) = no_function("slider");
|
||||
module slider(l=30, w=10, h=10, base=10, wall=5, ang=30, chamfer=2, anchor=BOTTOM, spin=0, orient=UP)
|
||||
{
|
||||
full_width = w + 2*wall;
|
||||
full_height = h + base;
|
||||
@@ -45,11 +46,11 @@ module slider(l=30, w=10, h=10, base=10, wall=5, ang=30, anchor=BOTTOM, spin=0,
|
||||
zrot(90)
|
||||
down(base+h/2) {
|
||||
// Base
|
||||
cuboid([full_width, l, base-get_slop()], chamfer=2, edges=[FRONT,BACK], except_edges=BOT, anchor=BOTTOM);
|
||||
cuboid([full_width, l, base-get_slop()], chamfer=chamfer, edges=[FRONT,BACK], except_edges=BOT, anchor=BOTTOM);
|
||||
|
||||
// Wall
|
||||
xflip_copy(offset=w/2+get_slop()) {
|
||||
cuboid([wall, l, full_height], chamfer=2, edges=RIGHT, except_edges=BOT, anchor=BOTTOM+LEFT);
|
||||
cuboid([wall, l, full_height], chamfer=chamfer, edges=RIGHT, except_edges=BOT, anchor=BOTTOM+LEFT);
|
||||
}
|
||||
|
||||
// Sliders
|
||||
|
||||
@@ -1046,7 +1046,7 @@ module shape_compare(eps=1/1024) {
|
||||
// Description:
|
||||
// Returns true if the `state` value indicates the current loop should continue. This is useful
|
||||
// when using C-style for loops to iteratively calculate a value. Used with `loop_while()` and
|
||||
// `loop_done()`. See [Looping Helpers](section-looping-helpers) for an example.
|
||||
// `loop_done()`. See [Looping Helpers](utility.scad#section-c-style-for-loop-helpers) for an example.
|
||||
// Arguments:
|
||||
// state = The loop state value.
|
||||
function looping(state) = state < 2;
|
||||
@@ -1062,7 +1062,7 @@ function looping(state) = state < 2;
|
||||
// Given the current `state`, and a boolean `continue` that indicates if the loop should still be
|
||||
// continuing, returns the updated state value for the the next loop. This is useful when using
|
||||
// C-style for loops to iteratively calculate a value. Used with `looping()` and `loop_done()`.
|
||||
// See [Looping Helpers](section-looping-helpers) for an example.
|
||||
// See [Looping Helpers](utility.scad#section-c-style-for-loop-helpers) for an example.
|
||||
// Arguments:
|
||||
// state = The loop state value.
|
||||
// continue = A boolean value indicating whether the current loop should progress.
|
||||
@@ -1080,7 +1080,7 @@ function loop_while(state, continue) =
|
||||
// Description:
|
||||
// Returns true if the `state` value indicates the loop is finishing. This is useful when using
|
||||
// C-style for loops to iteratively calculate a value. Used with `looping()` and `loop_while()`.
|
||||
// See [Looping Helpers](#5-looping-helpers) for an example.
|
||||
// See [Looping Helpers](utility.scad#section-c-style-for-loop-helpers) for an example.
|
||||
// Arguments:
|
||||
// state = The loop state value.
|
||||
function loop_done(state) = state > 0;
|
||||
|
||||
Reference in New Issue
Block a user