Merge pull request #1564 from amatulic/anachronist_isosurface

Formatting, centered Example 16, corrected math error in doc

isosurface.scad

@@ -33,7 +33,7 @@
 //   [fused filament fabrication](https://en.wikipedia.org/wiki/Fused_filament_fabrication). The gyroid
 //   isosurface is unbounded and periodic in all three dimensions.
 //   .
-//   This file provides modules and functions to create a VNF using metaballs, or from general isosurfaces.
+//   This file provides modules and functions to create a [VNF](vnf.scad) using metaballs, or from general isosurfaces.
 //   
 // Includes:
 //   include <BOSL2/std.scad>
@@ -1217,7 +1217,7 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 // Usage: As a function
 //   vnf = metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [convexity=], [show_stats=]);
 // Description:
-//   ![Metaball animation](https://raw.githubusercontent.com/BelfrySCAD/BOSL2/master/images/metaball_demo.png)
+//   ![Metaball animation](https://raw.githubusercontent.com/BelfrySCAD/BOSL2/master/images/metaball_demo.gif)
 //   .
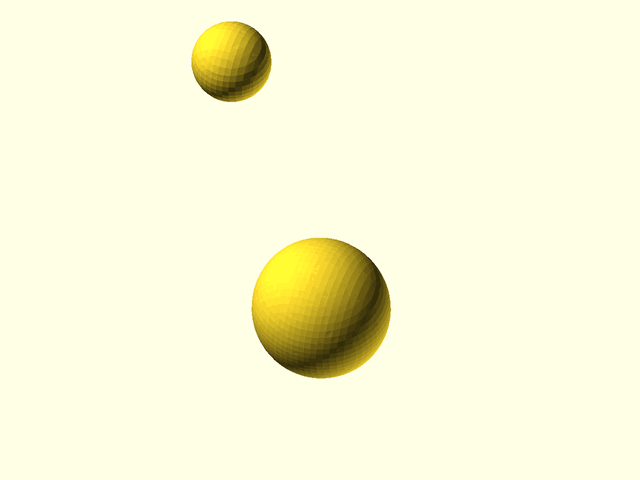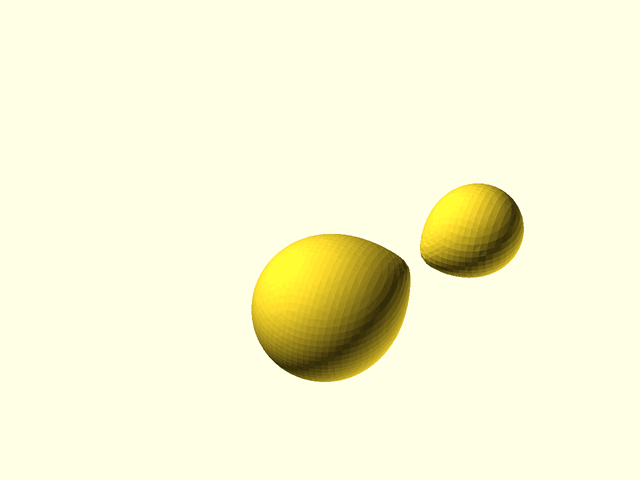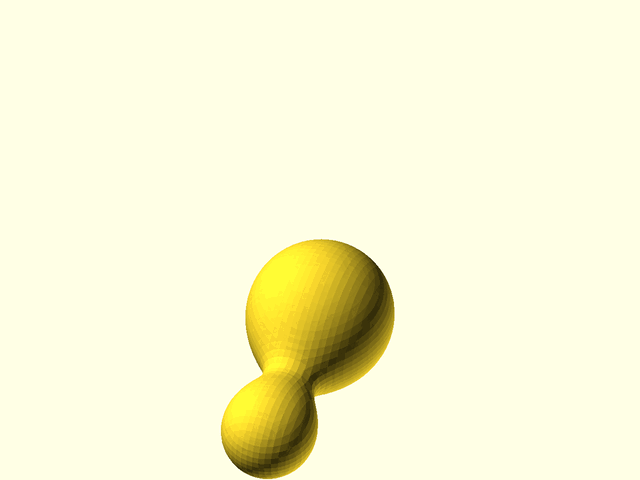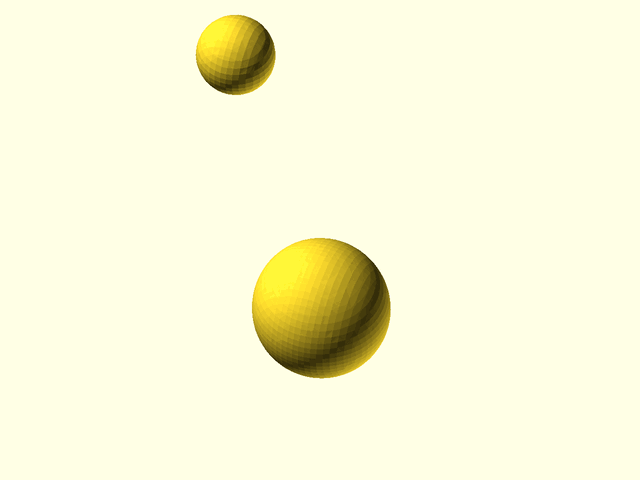
 //   [Metaballs](https://en.wikipedia.org/wiki/Metaballs), also known as "blobby objects",
 //   can produce smoothly varying blobs and organic forms. You create metaballs by placing metaball
@@ -1226,7 +1226,7 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   and melding together. The closer the objects are, the more they blend and meld.
 //   .
 //   The simplest metaball specification is a 1D list of alternating transformation matrices and
-//   metaball functions: `[trans0, spec0, trans1, spec1, ... ]`.  The transformation matrix
+//   metaball functions: `[trans0, func0, trans1, func1, ... ]`. Each transformation matrix
 //   you supply can be constructed using the usual transformation commands such as {{up()}},
 //   {{right()}}, {{back()}}, {{move()}}, {{scale()}}, {{rot()}} and so on.  You can multiply
 //   the transformations together, similar to how the transformations can be applied
@@ -1236,10 +1236,19 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   scaling to produce an ellipse from a sphere, and you can even use {{skew()}} if desired. 
 //   When no transformation is needed, give `IDENT` as the transformation.
 //   .
-//   The `isovalue` parameter defaults to 1. If you increase it, all the objects in your model
-//   shrink, causing some melded objects to separate. If you decrease it, each metaball grows and
-//   melds more with others. Be aware that changing the isovalue affects **all** the metaballs and
-//   changes the entire model, possibly dramatically.
+//   The metaballs are evaluated over a bounding box defined by its minimum and maximum corners,
+//   `[[xmin,ymin,zmin],[xmax,ymax,zmax]]`. The contributions from **all** metaballs, even those outside
+//   the bounds, are evaluated over the bounding box. This bounding box is divided into voxels of the
+//   specified `voxel_size`. Smaller voxels produce a finer, smoother result at the expense of
+//   execution time. If the voxel size doesn't exactly divide your specified bounding box, then
+//   the bounding box is enlarged to contain whole voxels, and centered on your requested box. If
+//   the bounding box clips a metaball and `closed=true` (the default), the object is closed at the
+//   intersection surface. Setting `closed=false` causes the [VNF](vnf.scad) to end at the bounding box,
+//   resulting in a non-manifold shape with holes, exposing the inside of the object.
+//   .
+//   For metaballs with flat surfaces (the ends of `mb_cyl()`, and `mb_cuboid()` with `squareness=1`),
+//   avoid letting any side of the bounding box coincide with one of these flat surfaces, otherwise
+//   unpredictable triangulation around the edge may result. This practice would increase run-time also.
 //   .
 //   You can create metaballs in a variety of standard shapes using the predefined functions
 //   listed below. If you wish, you can also create custom metaball shapes using your own functions
@@ -1269,18 +1278,23 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   The `negative` parameter, if set to `true`, creates a negative metaball, which can create
 //   hollows or dents in other metaballs, or swallow other metaballs entirely, making them disappear.
 //   Negative metaballs are always below the isovalue, so they are never directly visible;
-//   only their effects are visible. See Examples 7 and 8.
+//   only their effects are visible. See Examples 15 and 16.
+//   .
+//   The `isovalue` parameter defaults to 1. If you increase it, all the objects in your model
+//   shrink, causing some melded objects to separate. If you decrease it, each metaball grows and
+//   melds more with others. Be aware that changing the isovalue affects **all** the metaballs and
+//   changes the entire model, possibly dramatically.
 //   .
 //   For complicated metaball assemblies you may wish to repeat a structure in different locations or
-//   otherwise transformed. Nesting metaball specifications are supported:
-//   Instad of specifying a transform and function, you specify a transform and then a metaball
+//   otherwise transformed. Nested metaball specifications are supported:
+//   Instead of specifying a transform and function, you specify a transform and then another metaball
 //   specification. For example, you could set `finger=[t0,f0,t1,f1,t2,f2]` and then set
-//   `hand=[u0,finger,u1,finger,...]` and then invoke metaball with `[s0, hand]`.
-//   In effect, any list of metaballs can be treated as a single metaball.
+//   `hand=[u0,finger,u1,finger,...]` and then invoke `metaballs()` with `[s0, hand]`.
+//   In effect, any metaball specification array can be treated as a single metaball.
 //   This is a powerful technique that lets you make groups of metaballs that you can use as individual
 //   metaballs in other groups, and can make your code compact and simpler to understand. See Example 21.
 //   .
-//   ###Built-in metaball functions
+//   ***Built-in metaball functions***
 //   .
 //   Several metaballs are defined for you to use in your models. 
 //   All of the built-in metaballs take positional and named parameters that specify the size of the
@@ -1292,23 +1306,23 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   if `isovalue<1` and smaller than their specified sizes if `isovalue>1`.
 //   .
 //   All of the built-in functions all accept these named arguments, which are not repeated in the list below:
-//   * `cutoff` &em; positive value giving the distance beyond which the metaball does not interact with other balls.  Cutoff is measured from the object's center unless otherwise noted below.  Default: INF
-//   * `influence` &em; a positive number specifying the strength of interaction this ball has with other balls.  Default: 1
-//   * `negative` &em; when true, create a negative metaball. Default: false
+//   * `cutoff` &mdash; positive value giving the distance beyond which the metaball does not interact with other balls.  Cutoff is measured from the object's center unless otherwise noted below.  Default: INF
+//   * `influence` &mdash; a positive number specifying the strength of interaction this ball has with other balls.  Default: 1
+//   * `negative` &mdash; when true, create a negative metaball. Default: false
 //   .
-//   The built in metaballs functions are listed below. As usual, named arguments appear in the parameter list with a trailing `=`.
+//   The built in metaballs functions are listed below. As usual, arguments without a trailing `=` can be used positionally; arguments with a trailing `=` must be used as named arguments.
 //   The list of examples below illustrates each type of metaball interacting with another of the same type.
 //   .
-//   * `mb_sphere(r|d=)` &em; spherical metaball, with radius r or diameter d.  You can create an ellipsoid using `scale()` as the last transformation entry of the metaball `spec` array. 
-//   * `mb_cuboid(size, [squareness=])` &em; cuboid metaball with rounded edges and corners. The corner sharpness is controlled by the `squareness` parameter ranging from 0 (spherical) to 1 (cubical), and defaults to 0.5. The `size` is a scalar that specifies the width of the cuboid shape between the face centers. Except when `squareness=1`, the faces are always a little bit curved.
-//   * `mb_cyl(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=], [rounding=])` &em; vertical cylinder or cone metaball with the same dimenional arguments as {{cyl()}}. At least one of the radius or diameter arguments is required. The `rounding` argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a fully rounded cylindrical shape, consider `mb_capsule()` or `mb_disk()`, which are less flexible but have faster execution times.  For this metaball, the cutoff is measured from surface of the cone with the specified dimensions.
-//   * `mb_disk(h|l|height|length, r|d=)` &em; rounded disk with flat ends. The diameter specifies the total diameter of the shape including the rounded sides and must be greater than its height.
-//   * `mb_capsule(h|l|height|length, r|d=)` &em; cylinder of radius `r` or diameter `d` with hemispherical caps. The height or length specifies the **total** height including the rounded ends.
-//   * `mb_connector(p1, p2, r|d=)` &em; a connecting rod of radius `r` or diameter `d` with hemispherical caps (like `mb_capsule()`), but specified to connect point `p1` to point `p2` (where `p1` and `p2` must be different 3D vectors). The specified points are at the centers of the two capping hemispheres. You may want to set `influence` quite low; the connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear large and swollen unless `influence` is reduced.
-//   * `mb_torus([r_maj|d_maj=], [r_min|d_min=], [or=|od=], [ir=|id=])` &em; torus metaball oriented perpendicular to the z axis. You can specify the torus dimensions using the same arguments as {{torus()}}; that is, major radius (or diameter) with `r_maj` or `d_maj`, and minor radius and diameter using `r_min` or `d_min`. Alternatively you can give the inner radius or diameter with `ir` or `id` and the outer radius or diameter with `or` or `od`. Both major and minor radius/diameter must be specified regardless of how they are named.
-//   *`mb_octahedron(r|d=])` &em; octahedral metaball with sharp edges and corners. The `r` parameter specifies the distance from center to tip. The vertex parameter specifies the distance between the two opposite tips.
+//   * `mb_sphere(r|d=)` &mdash; spherical metaball, with radius r or diameter d.  You can create an ellipsoid using `scale()` as the last transformation entry of the metaball `spec` array. 
+//   * `mb_cuboid(size, [squareness=])` &mdash; cuboid metaball with rounded edges and corners. The corner sharpness is controlled by the `squareness` parameter ranging from 0 (spherical) to 1 (cubical), and defaults to 0.5. The `size` is a scalar that specifies the width of the cuboid shape between the face centers. Except when `squareness=1`, the faces are always a little bit curved.
+//   * `mb_cyl(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=], [rounding=])` &mdash; vertical cylinder or cone metaball with the same dimenional arguments as {{cyl()}}. At least one of the radius or diameter arguments is required. The `rounding` argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a fully rounded cylindrical shape, consider `mb_capsule()` or `mb_disk()`, which are less flexible but have faster execution times.  For this metaball, the cutoff is measured from surface of the cone with the specified dimensions.
+//   * `mb_disk(h|l|height|length, r|d=)` &mdash; rounded disk with flat ends. The diameter specifies the total diameter of the shape including the rounded sides and must be greater than its height.
+//   * `mb_capsule(h|l|height|length, r|d=)` &mdash; cylinder of radius `r` or diameter `d` with hemispherical caps. The height or length specifies the **total** height including the rounded ends.
+//   * `mb_connector(p1, p2, r|d=)` &mdash; a connecting rod of radius `r` or diameter `d` with hemispherical caps (like `mb_capsule()`), but specified to connect point `p1` to point `p2` (where `p1` and `p2` must be different 3D vectors). The specified points are at the centers of the two capping hemispheres. You may want to set `influence` quite low; the connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear large and swollen unless `influence` is reduced.
+//   * `mb_torus([r_maj|d_maj=], [r_min|d_min=], [or=|od=], [ir=|id=])` &mdash; torus metaball oriented perpendicular to the z axis. You can specify the torus dimensions using the same arguments as {{torus()}}; that is, major radius (or diameter) with `r_maj` or `d_maj`, and minor radius and diameter using `r_min` or `d_min`. Alternatively you can give the inner radius or diameter with `ir` or `id` and the outer radius or diameter with `or` or `od`. Both major and minor radius/diameter must be specified regardless of how they are named.
+//   *`mb_octahedron(r|d=])` &mdash; octahedral metaball with sharp edges and corners. The `r` parameter specifies the distance from center to tip. The vertex parameter specifies the distance between the two opposite tips.
 //   .
-//   ###Metaball functions and user defined functions
+//   ***Metaball functions and user defined functions***
 //   .
 //   Each metaball function is defined as a function of a 3-vector that gives the value of the metaball function
 //   for that point in space. As is common in metaball implementations, we define the built-in metaballs using an
@@ -1318,24 +1332,14 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   object, and decreasing the isovalue grows the object.
 //   .
 //   In order to adjust interaction strength, the influence parameter applies an exponent, so if `influence=a`
-//   then the decay becomes $1/d^{1/a}$. This means, for example, that if you set influence to 2 you get a
+//   then the decay becomes $1/d^{1/a}$. This means, for example, that if you set influence to 0.5 you get a
 //   $1/d^2$ falloff. Changing this exponent changes how the balls interact.
 //   .
 //   You can pass a custom function as a [function literal](https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/User-Defined_Functions_and_Modules#Function_literals)
 //   that takes a single argument (a 3-vector) and returns a single numerical value. 
 //   The returned value should define a function where in isovalue range [c,INF] defines a bounded object. See Example 19.
 //   .
-//   ###Voxel size and bounding box
-//   .
-//   The metaballs are evaluated over a bounding box defined by its minimum and maximum corners,
-//   `[[xmin,ymin,zmin],[xmax,ymax,zmax]]`. The contributions from **all** metaballs, even those outside
-//   the bounds, are evaluated over the bounding box. This bounding box is divided into voxels of the
-//   specified `voxel_size`. Smaller voxels produce a finer, smoother result at the expense of
-//   execution time. If the voxel size doesn't exactly divide your specified bounding box, then
-//   the bounding box is enlarged to contain whole voxels, and centered on your requested box. If
-//   the bounding box clips a metaball and `closed=true` (the default), the object is closed at the
-//   intersection surface. Setting `closed=false` causes the VNF to end at the bounding box,
-//   resulting in a non-manifold shape with holes, exposing the inside of the object.
+//   ***Voxel size and bounding box***
 //   .
 //   The `voxel_size` and `bounding_box` parameters affect the run time, which can be long.
 //   A voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the
@@ -1350,10 +1354,6 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   same run time but increase the resolution. You can also set the parameter `show_stats=true` to
 //   get the bounds of the voxels containing the generated surfaces.
 //   .
-//   For metaballs with flat surfaces (the ends of `mb_cyl()`, and `mb_cuboid()` with `squareness=1`),
-//   avoid letting any side of the bounding box coincide with one of these flat surfaces, otherwise
-//   unpredictable triangulation around the edge may result. This practice would increase run-time also.
-//   .
 //   The point list in the returned VNF structure contains many duplicated points. This is not a
 //   problem for rendering the shape, but if you want to eliminate these, you can pass
 //   the structure to {{vnf_merge_points()}}. Additionally, flat surfaces (often
@@ -1381,20 +1381,26 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 // Named Anchors:
 //   "origin" = Anchor at the origin, oriented UP.
 // Example(3D,NoAxes): Two spheres interacting.
-//   metaballs([
+//   spec = [
 //       left(9), mb_sphere(5),
 //       right(9), mb_sphere(5)
-//       ], 0.5, [[-16,-7,-7], [16,7,7]]);
+//   ];
+//   metaballs(spec, voxel_size=0.5,
+//       bounding_box=[[-16,-7,-7], [16,7,7]]);
 // Example(3D,NoAxes): Two rounded cuboids interacting.
-//   metaballs([
+//   spec = [
 //       move([-8,-5,-5]), mb_cuboid(10),
 //       move([8,5,5]), mb_cuboid(10)
-//       ], 0.5, [[-15,-12,-12], [15,12,12]]);
+//   ];
+//   metaballs(spec, voxel_size=0.5,
+//       bounding_box=[[-15,-12,-12], [15,12,12]]);
 // Example(3D,NoAxes): Two rounded `mb_cyl()` cones interacting.
-//   metaballs([
+//   spec = [
 //       left(10), mb_cyl(15, r1=8, r2=5, rounding=3),
 //       right(10), mb_cyl(15, r1=8, r2=5, rounding=3)
-//       ], 0.5, [[-19,-9,-10], [19,9,10]]);
+//   ];
+//   metaballs(spec, voxel_size=0.5,
+//       bounding_box=[[-19,-9,-10], [19,9,10]]);
 // Example(3D,NoAxes): Two disks interacting.
 //   metaballs([
 //       move([-10,0,2]), mb_disk(5,9),
@@ -1406,11 +1412,13 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //       move([8,0,-4])*yrot(90), mb_capsule(16,3)
 //       ], 0.5, [[-17,-5,-8], [17,5,8]]);
 // Example(3D,NoAxes): A sphere with two connectors.
-//   metaballs([
+//   spec = [
 //       left(20), mb_sphere(6),
 //       IDENT, mb_connector([-20,0,0], [0,0,10], 2, influence=0.5),
 //       IDENT, mb_connector([0,0,10], [0,-10,0], 2, influence=0.5)
-//       ], 0.5, [[-27,-13,-7], [4,7,14]]);
+//   ];
+//   metaballs(spec, voxel_size=0.5,
+//       bounding_box=[[-27,-13,-7], [4,7,14]]);
 // Example(3D,NoAxes): Interaction between two tori in different orientations.
 //    spec = [
 //        move([-10,0,17]),        mb_torus(r_maj=6, r_min=2),
@@ -1458,7 +1466,7 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   boundingbox = [[-30,-19,-19], [30,19,19]];
 //   metaballs(spec, voxelsize, boundingbox,
 //       isovalue=2);
-// Example(3D,VPD=110): Keeping `isovalue=2`, the influence of the tiny sphere has been set quite high, to 10. Notice that the tiny sphere does not change in size, but its contribution to its surroundings has dramatically increased, causing the two other spheres to grow and meld into each other. The `influence` argument on a small metaball affects its surroundings more than itself.
+// Example(3D,VPD=110): Keeping `isovalue=2`, the influence of the tiny sphere has been set quite high, to 10. Notice that the tiny sphere shrinks a bit, but it has dramatically increased its contribution to its surroundings, causing the two other spheres to grow and meld into each other. The `influence` argument on a small metaball affects its surroundings more than itself.
 //   spec = [
 //      move([-15,0,0]), mb_sphere(10),
 //      move([15,0,0]),  mb_sphere(10),
@@ -1490,7 +1498,7 @@ function mb_torus(r_maj, r_min, cutoff=INF, influence=1, negative=false, d_maj,
 //   boundingbox = [[-7,-6,-6], [3,6,6]];
 //   #metaballs(spec, voxelsize, boundingbox, isovalue);
 //   color("green") move_copies(centers) sphere(d=1, $fn=16);
-// Example(3D,VPD=100): When a positive and negative metaball interact, the negative metaball reduces the influence of the positive one, causing it to shrink but not disappear because its contribution approaches infinity at its center. In this example we have a large positive metaball near a small negative metaball at the origin. The negative ball as high influence and a cutoff limiting its influence to 20 units. The negative metaball influences the positive one up to the cutoff, causing the positive metaball to appear smaller inside the cutoff range, and appear its normal size outside the cutoff range. The positive metaball has a small dimple at the origin (the center of the negative metaball) because it cannot overcome the infinite negative contribution of the negative metaball at the origin.
+// Example(3D,VPD=105,VPT=[3,5,4.7]): When a positive and negative metaball interact, the negative metaball reduces the influence of the positive one, causing it to shrink but not disappear because its contribution approaches infinity at its center. In this example we have a large positive metaball near a small negative metaball at the origin. The negative ball as high influence and a cutoff limiting its influence to 20 units. The negative metaball influences the positive one up to the cutoff, causing the positive metaball to appear smaller inside the cutoff range, and appear its normal size outside the cutoff range. The positive metaball has a small dimple at the origin (the center of the negative metaball) because it cannot overcome the infinite negative contribution of the negative metaball at the origin.
 //   spec = [
 //       back(10), mb_sphere(20),
 //       IDENT, mb_sphere(2, influence = 30, cutoff = 20, negative = true),
@@ -1725,7 +1733,7 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
 //   "intersect" = Anchors to the surface of the shape.
 // Named Anchors:
 //   "origin" = Anchor at the origin, oriented UP.
-// Example(3D,ThrownTogether,NoAxes): A gyroid is an isosurface defined by all the zero values of a 3D periodic function. To illustrate what the surface looks like, `closed=false` has been set to expose both sides of the surface. The surface is periodic and tileable along all three axis directions. This a non-manifold surface as displayed, not useful for 3D modeling. This example also demonstrates using an additional parameters in the field function beyond just x,y,z; in this case controls the wavelength of the gyroid.
+// Example(3D,ThrownTogether,NoAxes): A gyroid is an isosurface defined by all the zero values of a 3D periodic function. To illustrate what the surface looks like, `closed=false` has been set to expose both sides of the surface. The surface is periodic and tileable along all three axis directions. This a non-manifold surface as displayed, not useful for 3D modeling. This example also demonstrates using an additional parameter in the field function beyond just x,y,z; in this case controls the wavelength of the gyroid.
 //   function gyroid(x,y,z, wavelength) = let(
 //       p = 360/wavelength,
 //       px = p*x, py = p*y, pz = p*z