mirror of
https://github.com/revarbat/BOSL2.git
synced 2025-10-01 21:26:47 +02:00
fixed mb_octahedron size, fixed doc issues
This commit is contained in:
@@ -23,7 +23,7 @@
|
||||
// .
|
||||
// In general, an isosurface can be defined using any function of three variables $x, y, z$.
|
||||
// The isosurface of a function $f(x,y,z)$ is the set of points where $f(x,y,z)=c$ for some constant
|
||||
// value $c$. Such a function is also known as an "implied surface" because the function *implies* a
|
||||
// value $c$. Such a function is also known as an "implicit surface" because the function *implies* a
|
||||
// surface of constant value within a volume of space. The constant $c$ is referred to as the "isovalue".
|
||||
// Changing the isovalue changes the position of the isosurface, depending on how the function is
|
||||
// defined. Because metaballs are isosurfaces, they also have an isovalue. The isovalue is also known
|
||||
@@ -983,6 +983,7 @@ function _mb_cuboid_full(point, inv_size, xp, ex, cutoff, neg) = let(
|
||||
function mb_cuboid(size, squareness=0.5, cutoff=INF, influence=1, negative=false) =
|
||||
assert(is_num(cutoff) && cutoff>0, "\ncutoff must be a positive number.")
|
||||
assert(is_finite(influence) && influence>0, "\ninfluence must be a positive number.")
|
||||
assert(squareness>=0 && squareness<=1, "\nsquareness must be inside the range [0,1].")
|
||||
assert((is_finite(size) && size>0) || (is_vector(size) && all_positive(size)), "\nsize must be a positive number or a 3-vector of positive values.")
|
||||
let(
|
||||
xp = _squircle_se_exponent(squareness),
|
||||
@@ -1288,17 +1289,20 @@ function _mb_octahedron_full(point, invr, xp, cutoff, ex, neg) =
|
||||
|
||||
function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=false, d) =
|
||||
assert(is_num(cutoff) && cutoff>0, "\ncutoff must be a positive number.")
|
||||
assert(squareness>=0 && squareness<=1, "\nsquareness must be inside the range [0,1].")
|
||||
assert(is_finite(influence) && is_num(influence) && influence>0, "\ninfluence must be a positive number.")
|
||||
let(
|
||||
xp = _squircle_se_exponent(squareness),
|
||||
r = get_radius(r=r,d=d),
|
||||
dummy=assert(is_finite(r) && r>0, "\ninvalid radius or diameter."),
|
||||
cf = let(s=squareness, s2=s*s) -0.299215*s*s2 + 0.737254*s2 - 0.59552*s + 1.1577,
|
||||
rcor = cf*r, // apply correction factor to r based on squareness
|
||||
neg = negative ? -1 : 1
|
||||
)
|
||||
!is_finite(cutoff) && influence==1 ? function(point) _mb_octahedron_basic(point,1/r,xp,neg)
|
||||
: !is_finite(cutoff) ? function(point) _mb_octahedron_influence(point,1/r,xp,1/influence, neg)
|
||||
: influence==1 ? function(point) _mb_octahedron_cutoff(point,1/r,xp,cutoff,neg)
|
||||
: function(point) _mb_octahedron_full(point,1/r,xp,cutoff,1/influence,neg);
|
||||
!is_finite(cutoff) && influence==1 ? function(point) _mb_octahedron_basic(point,1/rcor,xp,neg)
|
||||
: !is_finite(cutoff) ? function(point) _mb_octahedron_influence(point,1/rcor,xp,1/influence, neg)
|
||||
: influence==1 ? function(point) _mb_octahedron_cutoff(point,1/rcor,xp,cutoff,neg)
|
||||
: function(point) _mb_octahedron_full(point,1/rcor,xp,cutoff,1/influence,neg);
|
||||
|
||||
|
||||
|
||||
@@ -1308,9 +1312,9 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// Topics: Metaballs, Isosurfaces, VNF Generators
|
||||
// See Also: isosurface()
|
||||
// Usage: As a module
|
||||
// metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// metaballs(spec, bounding_box, voxel_size, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// Usage: As a function
|
||||
// vnf = metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=]);
|
||||
// vnf = metaballs(spec, bounding_box, voxel_size, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=]);
|
||||
// Description:
|
||||
// 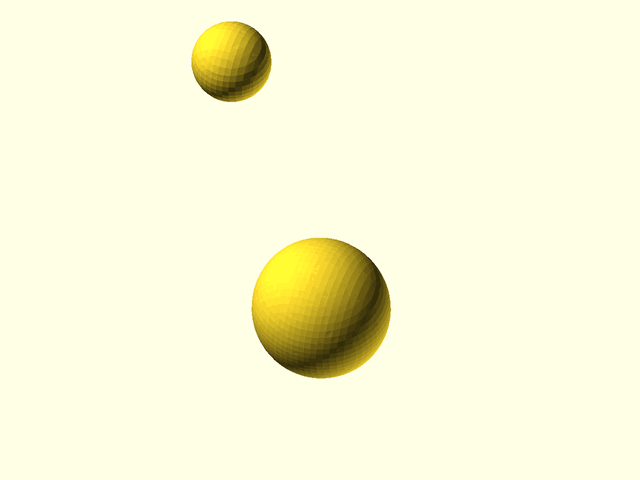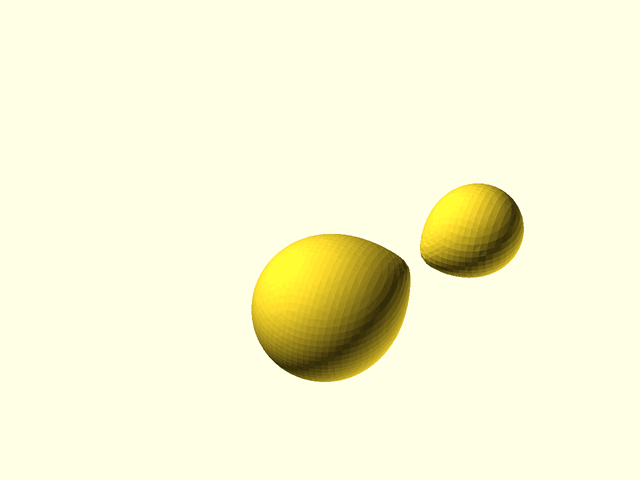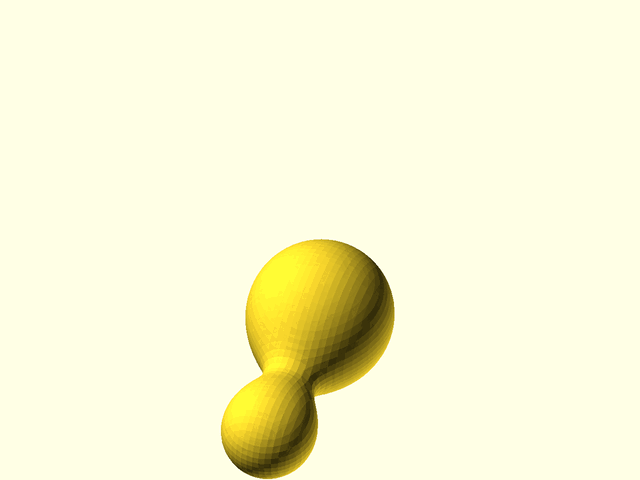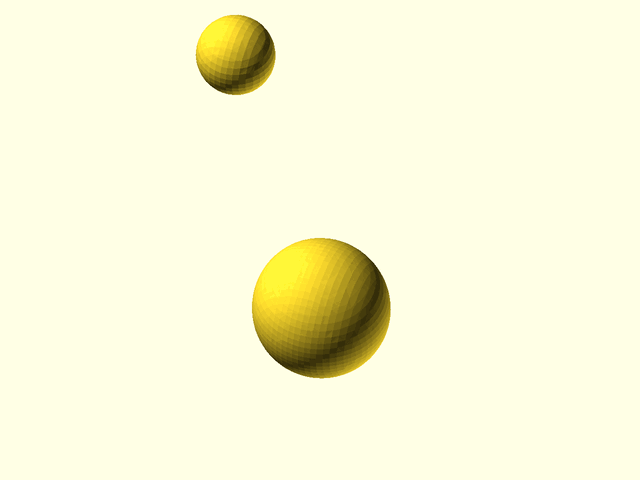
|
||||
// .
|
||||
@@ -1331,10 +1335,13 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// scaling to produce an ellipsoid from a sphere, and you can even use {{skew()}} if desired.
|
||||
// When no transformation is needed, give `IDENT` as the transformation.
|
||||
// .
|
||||
// The metaballs are evaluated over a bounding box, which can be a scalar-size cube or specified by its
|
||||
// minimum and maximum corners `[[xmin,ymin,zmin],[xmax,ymax,zmax]]`. The contributions from **all**
|
||||
// The metaballs are evaluated over a bounding box, which can be specified by its
|
||||
// minimum and maximum corners `[[xmin,ymin,zmin],[xmax,ymax,zmax]]`,
|
||||
// or specified as a scalar size of a cube centered on the origin. The contributions from **all**
|
||||
// metaballs, even those outside the box, are evaluated over the bounding box. This bounding box is
|
||||
// divided into voxels of the specified `voxel_size`, which can also be a scalar cube or a vector size.
|
||||
// Alternately, `voxel_count` may be specified to set the voxel size according to the requested
|
||||
// count of voxels in the bounding box.
|
||||
// Smaller voxels produce a finer, smoother result at the expense of execution time. By default, if the
|
||||
// voxel size doesn't exactly divide your specified bounding box, then the bounding box is enlarged to
|
||||
// contain whole voxels, and centered on your requested box. Alternatively, you may set
|
||||
@@ -1407,20 +1414,19 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// `isovalue > 1`.
|
||||
// .
|
||||
// The built-in metaball functions are listed below. As usual, arguments without a trailing `=` can be used positionally; arguments with a trailing `=` must be used as named arguments.
|
||||
// The examples below illustrates each type of metaball interacting with another of the same type.
|
||||
// .
|
||||
// * `mb_sphere(r|d=)` — spherical metaball, with radius r or diameter d. You can create an ellipsoid using `scale()` as the last transformation entry of the metaball `spec` array.
|
||||
// * `mb_cuboid(size, [squareness=])` — cuboid metaball with rounded edges and corners. The corner sharpness is controlled by the `squareness` parameter ranging from 0 (spherical) to 1 (cubical), and defaults to 0.5. The `size` specifies the width of the cuboid shape between the face centers; `size` may be a scalar or a vector, as in {{cuboid()}}. Except when `squareness=1`, the faces are always a little bit curved.
|
||||
// * `mb_cyl(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=], [rounding=])` — vertical cylinder or cone metaball with the same dimenional arguments as {{cyl()}}. At least one of the radius or diameter arguments is required. The `rounding` argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a fully rounded cylindrical shape, consider using `mb_capsule()` or `mb_disk()`, which are less flexible but have faster execution times.
|
||||
// * `mb_cyl(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=], [rounding=])` — vertical cylinder or cone metaball with the same dimensional arguments as {{cyl()}}. At least one of the radius or diameter arguments is required. The `rounding` argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a fully rounded cylindrical shape, consider using `mb_capsule()` or `mb_disk()`, which are less flexible but have faster execution times.
|
||||
// * `mb_disk(h|l|height|length, r|d=)` — rounded disk with flat ends. The diameter specifies the total diameter of the shape including the rounded sides, and must be greater than its height.
|
||||
// * `mb_capsule(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=])` — vertical cylinder or cone with rounded caps, using the same dimensional arguments as {{cyl()}}. The object resembles two spheres with a hull around them. The height or length specifies the distance between the spherical centers of the ends. Cutoff is measured from the line segment between the two cap centers.
|
||||
// * `mb_connector(p1, p2, [r|d=], [r1=|d1=], [r2=|d2=])` — a connecting rod of radius `r` or diameter `d` with hemispherical caps (like `mb_capsule()`), but specified to connect point `p1` to point `p2` (where `p1` and `p2` must be different 3D coordinates). As with `mb_capsule()`, the radius of each cap can be different, and the object resembles two spheres wrapped in a null. The points `p1` and `p2` are at the centers of the two round caps. The connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear swollen unless `influence` or `cutoff` is reduced. Reducing `cutoff` is preferable if feasible, because reducing `influence` can produce interpolation artifacts.
|
||||
// * `mb_capsule(h|l|height|length, [r|d=]` — vertical cylinder or cone with rounded caps, using the same dimensional arguments as {{cyl()}}. The object resembles a convex hull of two spheres. The height or length specifies the distance between the spherical centers of the ends.
|
||||
// * `mb_connector(p1, p2, [r|d=])` — a connecting rod of radius `r` or diameter `d` with hemispherical caps (like `mb_capsule()`), but specified to connect point `p1` to point `p2` (where `p1` and `p2` must be different 3D coordinates). As with `mb_capsule()`, the object resembles a convex hull of two spheres. The points `p1` and `p2` are at the centers of the two round caps. The connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear swollen unless `influence` or `cutoff` is reduced. Reducing `cutoff` is preferable if feasible, because reducing `influence` can produce interpolation artifacts.
|
||||
// * `mb_torus([r_maj|d_maj=], [r_min|d_min=], [or=|od=], [ir=|id=])` — torus metaball oriented perpendicular to the z axis. You can specify the torus dimensions using the same arguments as {{torus()}}; that is, major radius (or diameter) with `r_maj` or `d_maj`, and minor radius and diameter using `r_min` or `d_min`. Alternatively you can give the inner radius or diameter with `ir` or `id` and the outer radius or diameter with `or` or `od`. You must provide a combination of inputs that completely specifies the torus. If `cutoff` is applied, it is measured from the circle represented by `r_min=0`.
|
||||
// * `mb_octahedron(r|d=, [squareness=])` — octahedron metaball with rounded edges and corners. The corner sharpness is controlled by the `squareness` parameter ranging from 0 (spherical) to 1 (sharp), and defaults to 0.5. The radius `r` specifies the radius to the sharp-corner octahedron, while `d=` is the distance between two opposite tips. The actual shape is smaller when `squareness<1`, reducing to a sphere that would fit inside the full octahedron at `squareness=0`. Except when `squareness=1`, the faces are always curved.
|
||||
// .
|
||||
// In addition to the dimensional arguments described above, all of the built-in functions accept the
|
||||
// following named arguments:
|
||||
// * `cutoff` — positive value giving the distance beyond which the metaball does not interact with other balls. Cutoff is measured from the object's center unless otherwise noted above. Default: INF
|
||||
// * `cutoff` — positive value giving the distance beyond which the metaball does not interact with other balls. Cutoff is measured from the object's center. Default: INF
|
||||
// * `influence` — a positive number specifying the strength of interaction this ball has with other balls. Default: 1
|
||||
// * `negative` — when true, creates a negative metaball. Default: false
|
||||
// .
|
||||
@@ -1441,8 +1447,8 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// the object.
|
||||
// .
|
||||
// To adjust interaction strength, the influence parameter applies an exponent, so if `influence=a`
|
||||
// then the decay becomes $\frac{1}{d^{\frac 1 a}}$. This means, for example, that if you set influence to
|
||||
// 0.5 you get a $\frac{1}{d^2}$ falloff. Changing this exponent changes how the balls interact.
|
||||
// then the decay becomes $1/d^{1/a}$. This means, for example, that if you set influence to
|
||||
// 0.5 you get a $1/d^2$ falloff. Changing this exponent changes how the balls interact.
|
||||
// .
|
||||
// You can pass a custom function as a [function literal](https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/User-Defined_Functions_and_Modules#Function_literals)
|
||||
// that takes a single argument (a 3-vector) and returns a single numerical value.
|
||||
@@ -1454,14 +1460,14 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// .
|
||||
// ***Voxel size and bounding box***
|
||||
// .
|
||||
// The `voxel_size` and `bounding_box` parameters affect the run time, which can be long.
|
||||
// The size of the voxels and size of the bounding box affects the run time, which can be long.
|
||||
// A voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the
|
||||
// calculation and storage of 8,000,000 function values, and more processing and memory to generate
|
||||
// the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the number
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. Omitting both
|
||||
// `voxel_size` and `voxel_count` arguments automatically sets a voxel size such that approximately 10,000
|
||||
// voxels fit within your bounding box, which should be reasonable for initial preview. Because a bounding
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. If you don't
|
||||
// specify either `voxel_size` or `voxel_count`, then a default count of 10,000 voxels is used,
|
||||
// which should be reasonable for initial preview. Because a bounding
|
||||
// box that is too large wastes time computing function values that are not needed, you can also set the
|
||||
// parameter `show_stats=true` to get the actual bounds of the voxels intersected by the surface. With this
|
||||
// information, you may be able to decrease run time, or keep the same run time but increase the resolution.
|
||||
@@ -1479,11 +1485,11 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// and are not normally necessary.
|
||||
// Arguments:
|
||||
// spec = Metaball specification in the form `[trans0, spec0, trans1, spec1, ...]`, with alternating transformation matrices and metaball specs, where `spec0`, `spec1`, etc. can be a metaball function or another metaball specification. See above for more details, and see Example 23 for a demonstration.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]` specifying the minimum and maximum box corner coordinates. By default, the actual bounding box is enlarged if necessary to fit whole voxels, and centered around your requested box. Set `exact_bounds=true` to hold the box size fixed, in which case the voxel changes size instead.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]` specifying the minimum and maximum box corner coordinates. Unless you set `exact_bounds=true`, the bounding box size may be enlarged to fit whole voxels.
|
||||
// voxel_size = size of the voxel that is used to sample the bounding box volume. This can be undef, a scalar size for a cubical voxel, or a 3-vector if you want non-cubical voxels. For `undef`, the voxel size is set so that approximately `voxel_count` quantity of voxels fit inside the bounding box. If both `voxel_size=undef` and `voxel_count=undef`, then a fast preview is generated using about 10000 voxels. If you set `exact_bounds=true`, then bounding box is held fixed in size, and the voxel size is adjusted as needed so that whole voxels fit inside the bounding box.
|
||||
// voxel_count = Approximate quanity of voxels to have in the bounding box when `voxel_size` is not given. If both `voxel_size=undef` and `voxel_count=undef`, then a fast preview is generated using about 10000 voxels. Use with `show_stats=true` to see the corresponding voxel size.
|
||||
// isovalue = A scalar value specifying the isosurface value (threshold value) of the metaballs. At the default value of 1.0, the internal metaball functions are designd so the size arguments correspond to the size parameter (such as radius) of the metaball, when rendered in isolation with no other metaballs. Default: 1.0
|
||||
// ---
|
||||
// voxel_count = Approximate number of voxels in the bounding box. If `exact_bounds=true` then the voxels may not be cubes. Use with `show_stats=true` to see the corresponding voxel size. Default: 10000 (if `voxel_size` not set)
|
||||
// isovalue = A scalar value specifying the isosurface value (threshold value) of the metaballs. At the default value of 1.0, the internal metaball functions are designd so the size arguments correspond to the size parameter (such as radius) of the metaball, when rendered in isolation with no other metaballs. Default: 1.0
|
||||
// closed = When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face, possibly producing non-manfold metaballs with holes where the bounding box intersects them. Default: true
|
||||
// exact_bounds = When true, shrinks voxels as needed to fit whole voxels inside the requested bounding box. When false, enlarges `bounding_box` as needed to fit whole voxels of `voxel_size`, and centers the new bounding box over the requested box. Default: false
|
||||
// show_stats = If true, display statistics about the metaball isosurface in the console window. Besides the number of voxels that the surface passes through, and the number of triangles making up the surface, this is useful for getting information about a possibly smaller bounding box to improve speed for subsequent renders. Enabling this parameter has a small speed penalty. Default: false
|
||||
@@ -1597,7 +1603,7 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, boundingbox, voxel_size,
|
||||
// isovalue=2);
|
||||
// Example(3D,Med): Setting `influence` to less than 0.5 can cause interpolation artifacts in the surface. The only difference between these two spheres is `influence`. Both have `cutoff` set to prevent them from affecting each other. The sphere on the right has a low influence of 0.02, which translates to a falloff with distance $d$ proportional to $\frac{1}{d^50}$. That high exponent increases the *non-linear* nature of the function gradient at the isosurface, reducing the accuracy of the *linear* interpolation of where the the surface intersects each voxel, causing ridges to appear. You could use this to create a texture deliberately, but it is usually better to use `cutoff` to limit the range of influence rather than reducing `influence` significantly below 1.
|
||||
// Example(3D,Med): Setting `influence` to less than 0.5 can cause interpolation artifacts in the surface. The only difference between these two spheres is `influence`. Both have `cutoff` set to prevent them from affecting each other. The sphere on the right has a low influence of 0.02, which translates to a falloff with distance $d$ proportional to $1/d^{50}$. That high exponent increases the *non-linear* nature of the function gradient at the isosurface, reducing the accuracy of the *linear* interpolation of where the the surface intersects each voxel, causing ridges to appear. You could use this to create a texture deliberately, but it is usually better to use `cutoff` to limit the range of influence rather than reducing `influence` significantly below 1.
|
||||
// spec = [
|
||||
// left(10), mb_sphere(8, cutoff=10, influence=1),
|
||||
// right(10), mb_sphere(8, cutoff=10, influence=0.02)
|
||||
@@ -1635,7 +1641,7 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// voxel_size = 0.5;
|
||||
// boundingbox = [[-20,-4,-20], [20,30,20]];
|
||||
// metaballs(spec, boundingbox, voxel_size);
|
||||
// Example(3D,NoAxes): A sharp cube, a rounded cube, and a sharp octahedron interacting. Because the surface is generated through cubical voxels, voxel corners are always cut off, resulting in difficulty resolving some sharp edges.
|
||||
// Example(3D,NoAxes,VPD=80,VPT=[3,0,19]): A sharp cube, a rounded cube, and a sharp octahedron interacting. Because the surface is generated through cubical voxels, voxel corners are always cut off, resulting in difficulty resolving some sharp edges.
|
||||
// spec = [
|
||||
// move([-7,-3,27])*zrot(55), mb_cuboid(6, squareness=1),
|
||||
// move([5,5,21]), mb_cuboid(5),
|
||||
@@ -1837,7 +1843,7 @@ function mb_octahedron(r, squareness=0.5, cutoff=INF, influence=1, negative=fals
|
||||
// vsize = 0.85;
|
||||
// bbox = [[-45.5, -11.5, 0], [23, 11.5, 87.55]];
|
||||
// metaballs(spec, bbox, voxel_size=vsize);
|
||||
// Example(3D,Med,NoAxes): A model of a bunny, made from separate body components made with metaballs, with each component rendered at a different voxel size, and then combined together along with eyes and teeth. In this way, smaller bounding boxes can be defined for each component, which speeds up rendering. A bit more time is saved by saving the repeated components (ear, front leg, hind leg) in VNF structures, to render copies with {{vnf_polyhedron()}}.
|
||||
// Example(3D,Med,NoAxes,VPD=228,VPT=[1,-5,35]): A model of a bunny, made from separate body components made with metaballs, with each component rendered at a different voxel size, and then combined together along with eyes and teeth. In this way, smaller bounding boxes can be defined for each component, which speeds up rendering. A bit more time is saved by saving the repeated components (ear, front leg, hind leg) in VNF structures, to render copies with {{vnf_polyhedron()}}.
|
||||
// torso = [
|
||||
// up(20) * scale([1,1.2,2]), mb_sphere(10),
|
||||
// up(10), mb_sphere(5) // fatten lower torso
|
||||
@@ -1980,14 +1986,14 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// The array indices are in the order `[x][y][z]`.
|
||||
// .
|
||||
// The isovalue must be specified as a range `[c_min,c_max]`. The range can be finite or unbounded at one
|
||||
// end, with either `c_min=-INF` or `c_max=INF`. The returned object is the set of points `p` that
|
||||
// satisfy `c_min <= f(p) <= c_max`. If `f(p)` has values larger than `c_min` and values smaller than
|
||||
// end, with either `c_min=-INF` or `c_max=INF`. The returned object is the set of points `[x,y,z]` that
|
||||
// satisfy `c_min <= f(x,y,z) <= c_max`. If `f(x,y,z)` has values larger than `c_min` and values smaller than
|
||||
// `c_max`, then the result is a shell object with two bounding surfaces corresponding to the
|
||||
// isosurfaces at `c_min` and `c_max`. If `f(p) < c_max`
|
||||
// isosurfaces at `c_min` and `c_max`. If `f(x,y,z) < c_max`
|
||||
// everywhere (which is true when `c_max = INF`), then no isosurface exists for `c_max`, so the object
|
||||
// has only one bounding surface: the one defined by `c_min`. This can result in a bounded object
|
||||
// like a sphere, or it can result an an unbounded object such as all the points outside of a sphere out
|
||||
// to infinity. A similar situation arises if `f(p) > c_min` everywhere (which is true when
|
||||
// to infinity. A similar situation arises if `f(x,y,z) > c_min` everywhere (which is true when
|
||||
// `c_min = -INF`). Setting isovalue to `[-INF,c_max]` or `[c_min,INF]` always produces an object with a
|
||||
// single bounding isosurface, which itself can be unbounded. To obtain a bounded object, think about
|
||||
// whether the function values inside your object are smaller or larger than your isosurface value. If
|
||||
@@ -2013,14 +2019,14 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// `[c1,c2]`, try changing it to `[c2,INF]` or `[-INF,c1]`. If you were using an unbounded range like
|
||||
// `[c,INF]`, try switching the range to `[-INF,c]`.
|
||||
// .
|
||||
// ***Run time:*** The `voxel_size` and `bounding_box` parameters affect the run time, which can be long.
|
||||
// ***Run time:*** The size of the voxels and size of the bounding box affects the run time, which can be long.
|
||||
// A voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the
|
||||
// calculation and storage of 8,000,000 function values, and more processing and memory to generate
|
||||
// the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the number
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. Omitting both
|
||||
// `voxel_size` and `voxel_count` arguments automatically sets a voxel size such that approximately 10,000
|
||||
// voxels fit within your bounding box, which should be reasonable for initial preview. Because a bounding
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. If you don't
|
||||
// specify voxel_size or voxel_count then metaballs uses a default voxel_count of 10000, which should be
|
||||
// reasonable for initial preview. Because a bounding
|
||||
// box that is too large wastes time computing function values that are not needed, you can also set the
|
||||
// parameter `show_stats=true` to get the actual bounds of the voxels intersected by the surface. With this
|
||||
// information, you may be able to decrease run time, or keep the same run time but increase the resolution.
|
||||
@@ -2037,10 +2043,10 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// Arguments:
|
||||
// f = The isosurface function literal or array. As a function literal, `x,y,z` must be the first arguments.
|
||||
// isovalue = A 2-vector giving an isovalue range. For an unbounded range, use `[-INF, max_isovalue]` or `[min_isovalue, INF]`.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]` specifying the minimum and maximum box corner coordinates. By default, the actual bounding box is enlarged if necessary to fit whole voxels, and centered around your requested box. Set `exact_bounds=true` to hold the box size fixed, in which case the voxel changes size instead. When `f` is an array of values, `bounding_box` cannot be supplied if `voxel_size` is supplied because the bounding box is already implied by the array size combined with `voxel_size`, in which case this implied bounding box is centered around the origin.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]` specifying the minimum and maximum box corner coordinates. Unless you set `exact_bounds=true`, the bounding box size may be enlarged to fit whole voxels. When `f` is an array of values, `bounding_box` cannot be supplied if `voxel_size` is supplied because the bounding box is already implied by the array size combined with `voxel_size`, in which case this implied bounding box is centered around the origin.
|
||||
// voxel_size = size of the voxel that is used to sample the bounding box volume. This can be undef, a scalar size for a cubical voxel, or a 3-vector if you want non-cubical voxels. For `undef`, the voxel size is set so that approximately `voxel_count` quantity of voxels fit inside the bounding box. If both `voxel_size=undef` and `voxel_count=undef`, then a fast preview is generated using about 10000 voxels. If you set `exact_bounds=true`, then bounding box is held fixed in size, and the voxel size is adjusted as needed so that whole voxels fit inside the bounding box.
|
||||
// ---
|
||||
// voxel_count = Approximate quanity of voxels to have in the bounding box when `voxel_size` is not given. If both `voxel_size=undef` and `voxel_count=undef`, then a fast preview is generated using about 10000 voxels. Use with `show_stats=true` to see the corresponding voxel size. Default: undef
|
||||
// voxel_count = Approximate number of voxels in the bounding box. If `exact_bounds=true` then the voxels may not be cubes. Use with `show_stats=true` to see the corresponding voxel size. Default: 10000 (if `voxel_size` not set)
|
||||
// closed = When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face and instead produce a non-manfold VNF that has holes. Default: true
|
||||
// reverse = When true, reverses the orientation of the VNF faces. Default: false
|
||||
// exact_bounds = When true, shrinks voxels as needed to fit whole voxels inside the requested bounding box. When false, enlarges `bounding_box` as needed to fit whole voxels of `voxel_size`, and centers the new bounding box over the requested box. Default: false
|
||||
@@ -2150,20 +2156,17 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// (x*y*z^3 - 3*x^2*z^2) / np^2 + np^2,
|
||||
// isovalue=[-INF,35], bounding_box=[[-32,-32,-14],[32,32,14]],
|
||||
// voxel_size = 0.8, show_box=true);
|
||||
// Example(3D,NoAxes): You can specify non-cubical voxels for efficiency. This example shows the result of two identical surface functions. The figure on the left uses a `voxel_size=1`, which washes out the detail in the z direction. The figure on the right shows the same shape with `voxel_size=[0.5,1,0.2]` to give a bit more resolution in the x direction and much more resolution in the z direction. This example runs about six times faster than if we used a cubical voxel of size 0.2 to capture the detail in only one axis at the expense of unnecessary detail in other axes.
|
||||
// Example(3D,Med,NoAxes,VPD=47,VPT=[0,0,2]): You can specify non-cubical voxels for efficiency. This example shows the result of two identical surface functions. The figure on the left uses a `voxel_size=1`, which washes out the detail in the z direction. The figure on the right shows the same shape with `voxel_size=[0.5,1,0.2]` to give a bit more resolution in the x direction and much more resolution in the z direction. This example runs about six times faster than if we used a cubical voxel of size 0.2 to capture the detail in only one axis at the expense of unnecessary detail in other axes.
|
||||
// function shape(x,y,z, r=5) =
|
||||
// r / sqrt(x^2 + 0.5*(y^2 + z^2)
|
||||
// + 0.5*r*cos(200*z));
|
||||
// r / sqrt(x^2 + 0.5*(y^2 + z^2) + 0.5*r*cos(200*z));
|
||||
// bbox = [[-6,-8,0], [6,8,7]];
|
||||
//
|
||||
// left(6) isosurface(function (x,y,z) shape(x,y,z),
|
||||
// isovalue=[1,INF], bounding_box=bbox,
|
||||
// voxel_size=1);
|
||||
// isovalue=[1,INF], bounding_box=bbox, voxel_size=1);
|
||||
//
|
||||
// right(6) isosurface(function (x,y,z) shape(x,y,z),
|
||||
// isovalue=[1,INF], bounding_box=bbox,
|
||||
// voxel_size=[0.5,1,0.2]);
|
||||
// Example(3D,NoAxes): Nonlinear functions with steep gradients between voxel corners at the isosurface value can show interpolation ridges because the surface position is approximated by a linear interpolation of a highly nonlinear function. The appearance of the artifacts depends on the combination of function, voxel size, and isovalue, and can look different in different circumstances. If your isovalue is positive, then you may be able to smooth out the artifacts by using the log of your function and the log of your isovalue range to get the same isosurface without artifacts. On the left, an isosurface around a steep nonlinear function (clipped on the left by the bounding box) exhibits severe interpolation artifacts. On the right, the log of the isosurface around the log of the function smooths it out nicely.
|
||||
// isovalue=[1,INF], bounding_box=bbox, voxel_size=[0.5,1,0.2]);
|
||||
// Example(3D,NoAxes,VPD=50,VPT=[2,0,1]): Nonlinear functions with steep gradients between voxel corners at the isosurface value can show interpolation ridges because the surface position is approximated by a linear interpolation of a highly nonlinear function. The appearance of the artifacts depends on the combination of function, voxel size, and isovalue, and can look different in different circumstances. If your isovalue is positive, then you may be able to smooth out the artifacts by using the log of your function and the log of your isovalue range to get the same isosurface without artifacts. On the left, an isosurface around a steep nonlinear function (clipped on the left by the bounding box) exhibits severe interpolation artifacts. On the right, the log of the isosurface around the log of the function smooths it out nicely.
|
||||
// bbox = [[0,-10,-5],[9,10,6]];
|
||||
//
|
||||
// function shape(x,y,z) =
|
||||
|
||||
Reference in New Issue
Block a user