mirror of
https://github.com/revarbat/BOSL2.git
synced 2025-08-20 18:32:04 +02:00
more doc changes, examples, minor bugfixes
This commit is contained in:
399
isosurface.scad
399
isosurface.scad
@@ -668,6 +668,7 @@ _MCFaceVertexIndices = [
|
||||
[1,3,7,5], // top, z=voxsize plane
|
||||
];
|
||||
|
||||
/*
|
||||
/// Pair of vertex indices for each edge on the clip face (using clip face indexing)
|
||||
_MCClipEdgeVertexIndices = [
|
||||
[0,1], [1,2], [2,3], [3,0]
|
||||
@@ -701,11 +702,12 @@ function _clipfacindex(f, isoval) =
|
||||
(f[1] > isoval ? 2 : 0) +
|
||||
(f[2] > isoval ? 4 : 0) +
|
||||
(f[3] > isoval ? 8 : 0);
|
||||
*/
|
||||
|
||||
/// return an array of face indices in _MCFaceVertexIndices if the voxel at coordinate v0 corresponds to the bounding box.
|
||||
/// return an array of face indices in _MCFaceVertexIndices if the voxel at coordinate v0 corresponds to the bounding box. voxsize is a 3-vector.
|
||||
function _bbox_faces(v0, voxsize, bbox) = let(
|
||||
a = v_abs(v0-bbox[0]),
|
||||
bb1 = bbox[1] - [voxsize,voxsize,voxsize],
|
||||
bb1 = bbox[1] - voxsize,
|
||||
b = v0-bb1
|
||||
) [
|
||||
if(a[0]<EPSILON) 1,
|
||||
@@ -729,16 +731,16 @@ function _bbox_faces(v0, voxsize, bbox) = let(
|
||||
/// cubeindex_isomin and cubeindex_isomax are the index IDs of the voxel corresponding to the min and max iso surface intersections.
|
||||
/// cf (corner function) is vector containing the 8 field strength values at each corner of the voxel cube.
|
||||
/// bfaces is an array of faces corresponding to the sides of the bounding box - this is empty most of the time; it has data only where the isosurface is clipped by the bounding box.
|
||||
/// The bounding box 'bbox' is expected to be quantized for the voxel size already.
|
||||
/// The bounding box 'bbox' is expected to be quantized for the voxel size already, and `voxsize` is a 3-vector.
|
||||
|
||||
function _isosurface_cubes(voxsize, bbox, fieldarray, fieldfunc, isovalmin, isovalmax, closed=true) = let(
|
||||
// get field intensities
|
||||
field = is_def(fieldarray)
|
||||
? fieldarray
|
||||
: let(v = bbox[0], hv = 0.5*voxsize, b1 = bbox[1]+[hv,hv,hv]) [
|
||||
for(x=[v.x:voxsize:b1.x]) [
|
||||
for(y=[v.y:voxsize:b1.y]) [
|
||||
for(z=[v.z:voxsize:b1.z])
|
||||
: let(v = bbox[0], hv = 0.5*voxsize, b1 = bbox[1]+hv) [
|
||||
for(x=[v.x:voxsize.x:b1.x]) [
|
||||
for(y=[v.y:voxsize.y:b1.y]) [
|
||||
for(z=[v.z:voxsize.z:b1.z])
|
||||
fieldfunc([x,y,z])
|
||||
]
|
||||
]
|
||||
@@ -748,9 +750,9 @@ function _isosurface_cubes(voxsize, bbox, fieldarray, fieldfunc, isovalmin, isov
|
||||
nz = len(field[0][0])-2,
|
||||
v0 = bbox[0]
|
||||
) [
|
||||
for(i=[0:nx]) let(x=v0[0]+voxsize*i)
|
||||
for(j=[0:ny]) let(y=v0[1]+voxsize*j)
|
||||
for(k=[0:nz]) let(z=v0[2]+voxsize*k)
|
||||
for(i=[0:nx]) let(x=v0[0]+i*voxsize.x)
|
||||
for(j=[0:ny]) let(y=v0[1]+j*voxsize.y)
|
||||
for(k=[0:nz]) let(z=v0[2]+k*voxsize.z)
|
||||
let(i1=i+1, j1=j+1, k1=k+1,
|
||||
cf = [ // cube corner field values clamped to ±1e9
|
||||
min(1e9,max(-1e9,field[i][j][k])),
|
||||
@@ -771,7 +773,7 @@ function _isosurface_cubes(voxsize, bbox, fieldarray, fieldfunc, isovalmin, isov
|
||||
cubefound_outer = len(bfaces)==0 ? false
|
||||
: let(
|
||||
bf = flatten([for(i=bfaces) _MCFaceVertexIndices[i]]),
|
||||
sumcond = len([for(b=bf) if(isovalmin<cf[b] && cf[b]<isovalmax) 1 ])
|
||||
sumcond = len([for(b=bf) if(isovalmin<cf[b] && cf[b]<=isovalmax) 1 ])
|
||||
) sumcond == len(bf), // true if full faces are inside
|
||||
cubeindex_isomin = cubefound_isomin ? _cubeindex(cf, isovalmin) : 0,
|
||||
cubeindex_isomax = cubefound_isomax ? _cubeindex(cf, isovalmax) : 0
|
||||
@@ -788,7 +790,7 @@ function _isosurface_cubes(voxsize, bbox, fieldarray, fieldfunc, isovalmin, isov
|
||||
|
||||
/// _isosurface_trangles() - called by isosurface()
|
||||
/// Given a list of voxel cubes structures, triangulate the isosurface(s) that intersect each cube and return a list of triangle vertices.
|
||||
function _isosurface_triangles(cubelist, cubesize, isovalmin, isovalmax, tritablemin, tritablemax) = [
|
||||
function _isosurface_triangles(cubelist, voxsize, isovalmin, isovalmax, tritablemin, tritablemax) = [
|
||||
for(cl=cubelist)
|
||||
let(
|
||||
v = cl[0], // voxel coord
|
||||
@@ -796,10 +798,10 @@ function _isosurface_triangles(cubelist, cubesize, isovalmin, isovalmax, tritabl
|
||||
cbidxmax = cl[2], // cube ID for isovalmax
|
||||
f = cl[3], // function values for each cube corner
|
||||
bbfaces = cl[4], // faces (if any) on the bounding box
|
||||
vcube = [ // cube corner vertex coordinates
|
||||
v, v+[0,0,cubesize], v+[0,cubesize,0], v+[0,cubesize,cubesize],
|
||||
v+[cubesize,0,0], v+[cubesize,0,cubesize],
|
||||
v+[cubesize,cubesize,0], v+[cubesize,cubesize,cubesize]
|
||||
vcube = [ // list of cube corner vertex coordinates
|
||||
v, v+[0,0,voxsize.z], v+[0,voxsize.y,0], v+[0,voxsize.y,voxsize.z],
|
||||
v+[voxsize.x,0,0], v+[voxsize.x,0,voxsize.z],
|
||||
v+[voxsize.x,voxsize.y,0], v+voxsize
|
||||
]
|
||||
)
|
||||
each [
|
||||
@@ -910,24 +912,24 @@ function _bbfacevertices(vcube, f, bbface, isovalmax, isovalmin) = let(
|
||||
|
||||
/// _showstats_isosurface() (Private function) - called by isosurface()
|
||||
/// Display statistics about isosurface
|
||||
function _showstats_isosurface(voxelsize, bbox, isoval, cubes, triangles, faces) = let(
|
||||
function _showstats_isosurface(voxsize, bbox, isoval, cubes, triangles, faces) = let(
|
||||
v = column(cubes, 0), // extract cube vertices
|
||||
x = column(v,0), // extract x values
|
||||
y = column(v,1), // extract y values
|
||||
z = column(v,2), // extract z values
|
||||
xmin = min(x),
|
||||
xmax = max(x)+voxelsize,
|
||||
xmax = max(x)+voxsize.x,
|
||||
ymin = min(y),
|
||||
ymax = max(y)+voxelsize,
|
||||
ymax = max(y)+voxsize.y,
|
||||
zmin = min(z),
|
||||
zmax = max(z)+voxelsize,
|
||||
zmax = max(z)+voxsize.z,
|
||||
ntri = len(faces),
|
||||
nvox = len(cubes)
|
||||
) echo(str("\nIsosurface statistics:\n Outer isovalue = ", isoval, "\n Voxel size = ", voxelsize,
|
||||
) echo(str("\nIsosurface statistics:\n Isovalue = ", isoval, "\n Voxel size = ", voxsize,
|
||||
"\n Voxels intersected by the surface = ", nvox,
|
||||
"\n Triangles = ", ntri,
|
||||
"\n VNF bounds = ", pointlist_bounds(triangles),
|
||||
"\n Requested bounding box for all data = ", bbox,
|
||||
"\n Bounds for all data = ", bbox,
|
||||
"\n Voxel bounding box for isosurface = ", [[xmin,ymin,zmin], [xmax,ymax,zmax]],
|
||||
"\n")) 0;
|
||||
|
||||
@@ -1292,9 +1294,9 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// Topics: Metaballs, Isosurfaces, VNF Generators
|
||||
// See Also: isosurface()
|
||||
// Usage: As a module
|
||||
// metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [convexity=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [auto_voxels=], [convexity=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// Usage: As a function
|
||||
// vnf = metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [convexity=], [show_stats=]);
|
||||
// vnf = metaballs(spec, voxel_size, bounding_box, [isovalue=], [closed=], [auto_voxels=], [convexity=], [show_stats=]);
|
||||
// Description:
|
||||
// 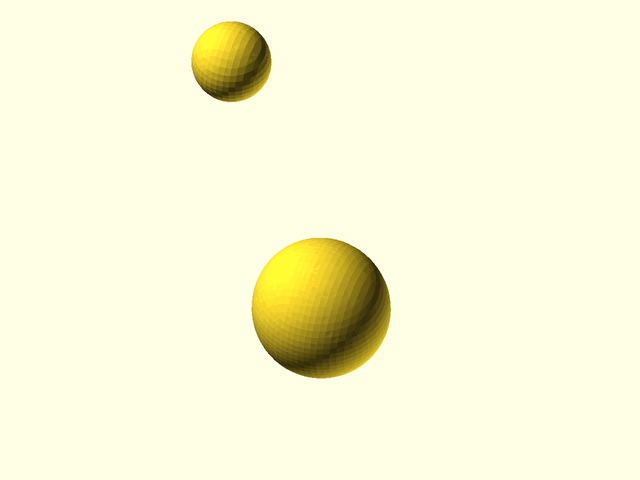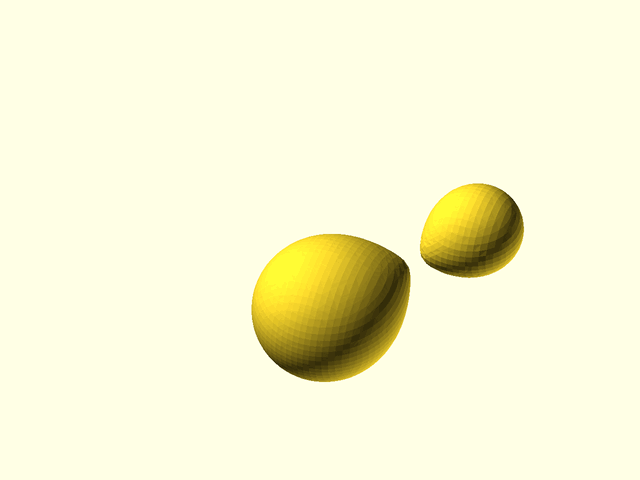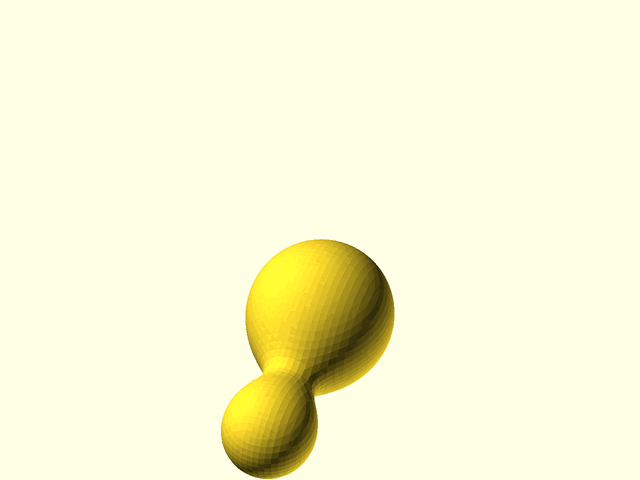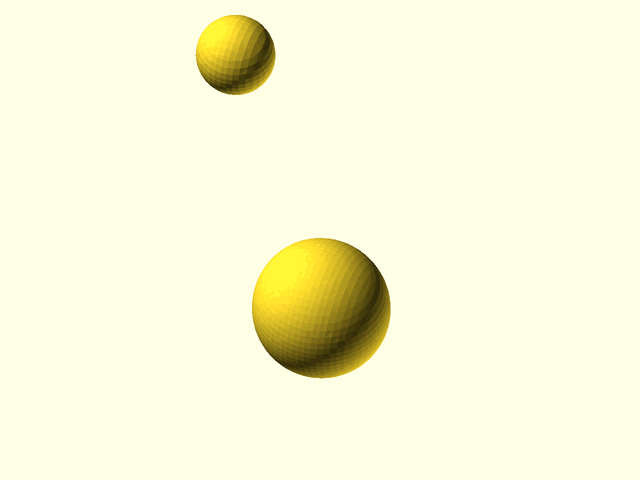
|
||||
// .
|
||||
@@ -1437,13 +1439,13 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// A voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the
|
||||
// calculation and storage of 8,000,000 function values, and more processing and memory to generate
|
||||
// the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the
|
||||
// number of voxels below 10,000 for preview, and adjust the voxel size smaller for final
|
||||
// rendering. A bounding box that is larger than your isosurface wastes time computing function
|
||||
// values that are not needed. If the metaballs fit completely within the bounding box, you can
|
||||
// set the parameter `show_stats=true` to get the bounds of the voxels containing the generated
|
||||
// surfacesto get an idea of a the optimal bounding box to use. You may be able to decrease run
|
||||
// time, or keep the same run time but increase the resolution. .
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the number
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. Setting
|
||||
// `voxel_size="auto"` sets a size such that approximately 8,000 voxels fit within your bounding box,
|
||||
// which should be reasonable for initial preview. Because a bounding box that is too large wastes time
|
||||
// computing function values that are not needed, you can also set the parameter `show_stats=true` to
|
||||
// get the actual bounds of the voxels intersected by the surface. With this information, you may be
|
||||
// able to decrease run time, or keep the same run time but increase the resolution.
|
||||
// .
|
||||
// The point list in the returned VNF structure contains many duplicated points. This is not a
|
||||
// problem for rendering the shape, but if you want to eliminate these, you can pass
|
||||
@@ -1454,12 +1456,13 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// and are not normally necessary.
|
||||
// Arguments:
|
||||
// spec = Metaball specification in the form `[trans0, spec0, trans1, spec1, ...]`, with alternating transformation matrices and metaball specs, where `spec0`, `spec1`, etc. can be a metaball function or another metaball specification. See above for more details, and see Example 22 for a demonstration.
|
||||
// voxel_size = scalar size of the voxel cube that is used to sample the bounding box volume.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]`, specifying the minimum and maximum box corner coordinates. The actual bounding box is enlarged if necessary to fit whole voxels, and centered around your requested box.
|
||||
// voxel_size = size of the voxel that is used to sample the bounding box volume. This can be "auto", a scalar size for a cubical voxel, or a 3-vector if you want non-cubical voxels. For "auto", the voxel size is set so that approximately `auto_voxels` (default 8000) quantity of voxels fit inside the bounding box. If you set `grow_bounds=false`, then bounding box is held fixed in size, and the voxel size is adjusted as needed so that whole voxels fit inside the bounding box.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]` specifying the minimum and maximum box corner coordinates. With the default `grow_bounds=true`, the actual bounding box is enlarged if necessary to fit whole voxels, and centered around your requested box.
|
||||
// isovalue = A scalar value specifying the isosurface value (threshold value) of the metaballs. At the default value of 1.0, the internal metaball functions are designd so the size arguments correspond to the size parameter (such as radius) of the metaball, when rendered in isolation with no other metaballs. Default: 1.0
|
||||
// ---
|
||||
// closed = When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face, possibly producing a non-manfold VNF that has holes. Default: true
|
||||
// closed = When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face, possibly producing non-manfold metaballs with holes where the bounding box intersects them. Default: true
|
||||
// show_stats = If true, display statistics about the metaball isosurface in the console window. Besides the number of voxels that the surface passes through, and the number of triangles making up the surface, this is useful for getting information about a possibly smaller bounding box to improve speed for subsequent renders. Enabling this parameter has a small speed penalty. Default: false
|
||||
// auto_voxels = Approximate quanity of voxels to have in the bounding box when `voxel_size="auto"`. Useful for fast preview of a reasonable number of voxels. Use with `show_stats=true` to see the corresponding voxel size. Default: 8000
|
||||
// convexity = (Module only) Maximum number of times a line could intersect a wall of the shape. Affects preview only. Default: 6
|
||||
// show_box = (Module only) display the requested bounding box as transparent. This box may appear slightly inside the bounds of the figure if the actual bounding box had to be expanded to accommodate whole voxels. Default: false
|
||||
// cp = (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
|
||||
@@ -1518,9 +1521,9 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// move([-10,0,17]), mb_torus(r_maj=6, r_min=2),
|
||||
// move([7,6,21])*xrot(90), mb_torus(r_maj=7, r_min=3)
|
||||
// ];
|
||||
// voxelsize = 0.5;
|
||||
// voxel_size = 0.5;
|
||||
// boundingbox = [[-19,-9,9], [18,10,32]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,NoAxes,VPR=[75,0,20]): Two octahedrons interacting.
|
||||
// metaballs([
|
||||
// move([-10,0,3]), mb_octahedron(8),
|
||||
@@ -1531,34 +1534,34 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// left(15), mb_sphere(10),
|
||||
// right(15), mb_sphere(10)
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,VPD=110): Adding a cutoff of 25 to the left sphere causes its influence to disappear completely 25 units away (5 units from the center of the right sphere). The left sphere is bigger because it still receives the full influence of the right sphere, but the right sphere is smaller because the left sphere has no contribution past 25 units. The right sphere is not abruptly cut off because the cutoff function is smooth and influence is normal. Setting cutoff too small can remove the interactions of one metaball from all other metaballs, leaving that metaball alone by itself.
|
||||
// spec = [
|
||||
// left(15), mb_sphere(10, cutoff=25),
|
||||
// right(15), mb_sphere(10)
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,VPD=110): Here, the left sphere has less influence in addition to a cutoff. Setting `influence=0.5` results in a steeper falloff of contribution from the left sphere. Each sphere has a different size and shape due to unequal contributions based on distance.
|
||||
// spec = [
|
||||
// left(15), mb_sphere(10, influence=0.5, cutoff=25),
|
||||
// right(15), mb_sphere(10)
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,VPD=110): In this example, we have two size-10 spheres as before and one tiny sphere of 1.5 units radius offset a bit on the y axis. With an isovalue of 1, this figure would appear similar to Example 9 above, but here the isovalue has been set to 2, causing the surface to shrink around a smaller volume values greater than 2. Remember, higher isovalue thresholds cause metaballs to shrink.
|
||||
// spec = [
|
||||
// left(15), mb_sphere(10),
|
||||
// right(15), mb_sphere(10),
|
||||
// fwd(15), mb_sphere(1.5)
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, voxelsize, boundingbox,
|
||||
// metaballs(spec, voxel_size, boundingbox,
|
||||
// isovalue=2);
|
||||
// Example(3D,VPD=110): Keeping `isovalue=2`, the influence of the tiny sphere has been set quite high, to 10. Notice that the tiny sphere shrinks a bit, but it has dramatically increased its contribution to its surroundings, causing the two other spheres to grow and meld into each other. The `influence` argument on a small metaball affects its surroundings more than itself.
|
||||
// spec = [
|
||||
@@ -1566,9 +1569,9 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// move([15,0,0]), mb_sphere(10),
|
||||
// move([0,-15,0]), mb_sphere(1.5, influence=10)
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-30,-19,-19], [30,19,19]];
|
||||
// metaballs(spec, voxelsize, boundingbox,
|
||||
// metaballs(spec, voxel_size, boundingbox,
|
||||
// isovalue=2);
|
||||
// Example(3D,NoAxes): A group of five spherical metaballs with different sizes. The parameter `show_stats=true` (not shown here) was used to find a compact bounding box for this figure.
|
||||
// spec = [ // spheres of different sizes
|
||||
@@ -1578,19 +1581,19 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// move([0,0,20]), mb_sphere(5),
|
||||
// move([20,20,10]), mb_sphere(7)
|
||||
// ];
|
||||
// voxelsize = 1.5;
|
||||
// voxel_size = 1.5;
|
||||
// boundingbox = [[-30,-31,-31], [32,31,31]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,NoAxes): A metaball can be negative. In this case we have two metaballs in close proximity, with the small negative metaball creating a dent in the large positive one. The positive metaball is shown transparent, and small spheres show the center of each metaball. The negative metaball isn't visible because its field is negative; the isosurface encloses only field values greater than the isovalue of 1.
|
||||
// centers = [[-1,0,0], [1.25,0,0]];
|
||||
// spec = [
|
||||
// move(centers[0]), mb_sphere(8),
|
||||
// move(centers[1]), mb_sphere(3, negative=true)
|
||||
// ];
|
||||
// voxelsize = 0.25;
|
||||
// voxel_size = 0.25;
|
||||
// isovalue = 1;
|
||||
// boundingbox = [[-7,-6,-6], [3,6,6]];
|
||||
// #metaballs(spec, voxelsize, boundingbox, isovalue);
|
||||
// %metaballs(spec, voxel_size, boundingbox, isovalue);
|
||||
// color("green") move_copies(centers) sphere(d=1, $fn=16);
|
||||
// Example(3D,VPD=105,VPT=[3,5,4.7]): When a positive and negative metaball interact, the negative metaball reduces the influence of the positive one, causing it to shrink, but not disappear because its contribution approaches infinity at its center. In this example we have a large positive metaball near a small negative metaball at the origin. The negative ball has high influence, and a cutoff limiting its influence to 20 units. The negative metaball influences the positive one up to the cutoff, causing the positive metaball to appear smaller inside the cutoff range, and appear its normal size outside the cutoff range. The positive metaball has a small dimple at the origin (the center of the negative metaball) because it cannot overcome the infinite negative contribution of the negative metaball at the origin.
|
||||
// spec = [
|
||||
@@ -1598,18 +1601,18 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// IDENT, mb_sphere(2, influence=30,
|
||||
// cutoff=20, negative=true),
|
||||
// ];
|
||||
// voxelsize = 0.5;
|
||||
// voxel_size = 0.5;
|
||||
// boundingbox = [[-20,-4,-20], [20,30,20]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,NoAxes): A cube, a rounded cube, and an octahedron interacting. Because the surface is generated through cubical voxels, voxel corners are always cut off, resulting in difficulty resolving some sharp edges.
|
||||
// spec = [
|
||||
// move([-7,-3,27])*zrot(55), mb_cuboid(6, squareness=1),
|
||||
// move([5,5,21]), mb_cuboid(5),
|
||||
// move([10,0,10]), mb_octahedron(5)
|
||||
// ];
|
||||
// voxelsize = 0.5; // a bit slow at this resolution
|
||||
// voxel_size = 0.5; // a bit slow at this resolution
|
||||
// boundingbox = [[-12,-9,3], [18,10,32]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,NoAxes,VPD=205,Med): A toy airplane, constructed only from metaball spheres with scaling. The bounding box is used to clip the wingtips, tail, and belly of the fuselage.
|
||||
// bounding_box = [[-55,-50,-5],[35,50,17]];
|
||||
// spec = [
|
||||
@@ -1619,13 +1622,13 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// move([-15,0,0])*scale([6,45,0.5]), mb_sphere(1) // wing
|
||||
// ];
|
||||
// voxel_size = 1;
|
||||
// metaballs(spec, voxel_size, bounding_box);
|
||||
// Example(3D,VPD=60,VPR=[57,0,50],VPT=[0.5,2,1.8]): Custom metaballs are an advanced technique in which you define your own metaball shape by passing a function literal that takes a single argument, a coordinate in space relative to the metaball center, called `point` but can be given any name. This distance vector is calculated internally and always passed to the function. Inside the function, it is converted to a scalar distance `dist`. The function literal expression sets all of your parameters. Only `point` is not set, and it becomes the single parameter to the function literal. The `spec` argument invokes your custom function as a function literal that passes `point` into it.
|
||||
// color("lightblue") metaballs(spec, voxel_size, bounding_box);
|
||||
// Example(3D,VPD=60,VPR=[57,0,50],VPT=[0.5,2,1.8]): Custom metaballs are an advanced technique in which you define your own metaball shape by passing a function literal that takes a single argument: a coordinate in space relative to the metaball center called `point` here, but can be given any name. This distance vector from the origin is calculated internally and always passed to the function. Inside the function, it is converted to a scalar distance `dist`. The function literal expression sets all of your parameters. Only `point` is not set, and it becomes the single parameter to the function literal. The `spec` argument invokes your custom function as a function literal that passes `point` into it.
|
||||
// function threelobe(point) =
|
||||
// let(
|
||||
// ang=atan2(point.y,point.x),
|
||||
// r = norm([point.x,point.y])*(1.3+cos(3*ang)),
|
||||
// dist=norm([point.z,r])
|
||||
// ang=atan2(point.y, point.x),
|
||||
// r=norm([point.x,point.y])*(1.3+cos(3*ang)),
|
||||
// dist=norm([point.z, r])
|
||||
// ) 3/dist;
|
||||
// metaballs(
|
||||
// spec = [
|
||||
@@ -1637,9 +1640,9 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// Example(3D,VPD=60,VPR=[57,0,50],VPT=[0.5,2,1.8]): Here is a function nearly identical to the previous example, introducing additional dimensional parameters into the function to control its size and number of lobes. The bounding box size here is as small as possible for calculation efficiency, but if you expiriment with this using different argument values, you should increase the bounding box along with voxel size.
|
||||
// function multilobe(point, size, lobes) =
|
||||
// let(
|
||||
// ang=atan2(point.y,point.x),
|
||||
// r = norm([point.x,point.y])*(1.3+cos(lobes*ang)),
|
||||
// dist=norm([point.z,r])
|
||||
// ang=atan2(point.y, point.x),
|
||||
// r=norm([point.x,point.y])*(1.3+cos(lobes*ang)),
|
||||
// dist=norm([point.z, r])
|
||||
// ) size/dist;
|
||||
// metaballs(
|
||||
// spec = [
|
||||
@@ -1678,10 +1681,10 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// left(9), mb_sphere(5),
|
||||
// right(9), noisy_sphere(r=5, noise_level=0.2)
|
||||
// ];
|
||||
// voxelsize = 0.5;
|
||||
// voxel_size = 0.5;
|
||||
// boundingbox = [[-16,-8,-8], [16,8,8]];
|
||||
// metaballs(spec, voxelsize, boundingbox);
|
||||
// Example(3D,Med,NoAxes,VPR=[55,0,0],VPD=200,VPT=[7,2,2]): A complex example using ellipsoids, a capsule, spheres, and a torus to make a tetrahedral object with rounded feet and a ring on top. The bottoms of the feet are flattened by clipping with the bottom of the bounding box. The center of the object is thick due to the contributions of three ellipsoids and a capsule converging. Designing an object like this using metaballs requires trial and error with low-resolution renders.
|
||||
// metaballs(spec, voxel_size, boundingbox);
|
||||
// Example(3D,Med,NoAxes,VPR=[55,0,0],VPD=200,VPT=[7,2,2]): A more complex example using ellipsoids, a capsule, spheres, and a torus to make a tetrahedral object with rounded feet and a ring on top. The bottoms of the feet are flattened by clipping with the bottom of the bounding box. The center of the object is thick due to the contributions of three ellipsoids and a capsule converging. Designing an object like this using metaballs requires trial and error with low-resolution renders.
|
||||
// include <BOSL2/polyhedra.scad>
|
||||
// tetpts = zrot(15, p = 22 * regular_polyhedron_info("vertices", "tetrahedron"));
|
||||
// tettransform = [ for(pt = tetpts) move(pt)*rot(from=RIGHT, to=pt)*scale([7,1.5,1.5]) ];
|
||||
@@ -1696,10 +1699,10 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// // feet
|
||||
// for(i=[0:2]) each [move(2.2*tetpts[i]), mb_sphere(5, cutoff=30)],
|
||||
// ];
|
||||
// voxelsize = 1;
|
||||
// voxel_size = 1;
|
||||
// boundingbox = [[-22,-32,-13], [36,32,46]];
|
||||
// // useful to save as VNF for copies and manipulations
|
||||
// vnf = metaballs(spec, voxelsize, boundingbox, isovalue=1);
|
||||
// vnf = metaballs(spec, voxel_size, boundingbox, isovalue=1);
|
||||
// vnf_polyhedron(vnf);
|
||||
// Example(3D,Med,NoAxes,VPR=[70,0,30],VPD=520,VPT=[0,0,80]): This example demonstrates grouping metaballs together and nesting them in lists of other metaballs, to make a crude model of a hand. Here, just one finger is defined, and a thumb is defined from one less joint in the finger. Individual fingers are grouped together with different positions and scaling, along with the thumb. Finally, this group of all fingers is used to combine with a rounded cuboid, with a slight ellipsoid dent subtracted to hollow out the palm, to make the hand.
|
||||
// joints = [[0,0,1], [0,0,85], [0,-5,125], [0,-16,157], [0,-30,178]];
|
||||
@@ -1710,7 +1713,7 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// thumb = [
|
||||
// for(i=[0:2]) each [
|
||||
// scale([1,1,1.2]),
|
||||
// mb_connector(joints[i], joints[i+1], 9+i/2, influence=.28)
|
||||
// mb_connector(joints[i], joints[i+1], 9+i/2, influence=0.28)
|
||||
// ]
|
||||
// ];
|
||||
// allfingers = [
|
||||
@@ -1726,22 +1729,46 @@ function mb_octahedron(r, cutoff=INF, influence=1, negative=false, d) =
|
||||
// move([-10,-95,50])*yrot(10)*scale([2,2,0.95]),
|
||||
// mb_sphere(r=15, cutoff=50, influence=1.5, negative=true)
|
||||
// ];
|
||||
// voxsize=2.5;
|
||||
// voxel_size=2.5;
|
||||
// bbox = [[-104,-40,-10], [79,18,188]];
|
||||
// metaballs(hand, voxsize, bbox, isovalue=1);
|
||||
// metaballs(hand, voxel_size, bbox, isovalue=1);
|
||||
// Example(3D,Med,NoAxes,VPR=[76,0,40],VPD=128,VPT=[4,-1,13]): A model of an elephant using cylinders, capsules, and disks.
|
||||
// legD1 = 11;
|
||||
// legD2 = 6;
|
||||
// spec = [
|
||||
// // legs
|
||||
// fwd(8)*left(10), mb_cyl(d1=legD1, d2=legD2, h=20),
|
||||
// fwd(8)*right(10), mb_cyl(d1=legD1, d2=legD2, h=20),
|
||||
// back(8)*left(10), mb_cyl(d1=legD1, d2=legD2, h=20),
|
||||
// back(8)*right(10), mb_cyl(d1=legD1, d2=legD2, h=20),
|
||||
// up(20)*yrot(90), mb_capsule(d=25,h=40, influence=0.5), // body
|
||||
// right(20)*up(25)*yrot(-20), mb_capsule(r=7, h = 25, influence=0.1), // head
|
||||
// right(23)*up(10)*yrot(15), mb_cyl(d1 = 3, d2=6, h = 15, influence=0.2), // trunk
|
||||
// // ears
|
||||
// right(20)*up(29)*fwd(11)*yrot(80)*scale([1.7,1,1]), mb_disk(r=5,h=6, influence=0.1),
|
||||
// right(20)*up(29)*back(11)*yrot(80)*scale([1.7,1,1]), mb_disk(r=5,h=6, influence=0.1),
|
||||
// // tusks
|
||||
// right(25)*up(13)*fwd(5)*yrot(135), mb_capsule(r=1, h = 10, influence=0.1),
|
||||
// right(25)*up(13)*back(5)*yrot(135), mb_capsule(r=1, h = 10, influence=0.1),
|
||||
// ];
|
||||
// bbox = [[-22,-17,-9], [30,17,39]];
|
||||
// metaballs(spec, voxel_size=1, bounding_box=bbox, isovalue=1);
|
||||
|
||||
module metaballs(spec, voxel_size, bounding_box, isovalue=1, closed=true, convexity=6, cp="centroid", anchor="origin", spin=0, orient=UP, atype="hull", show_stats=false, show_box=false) {
|
||||
vnf = metaballs(spec, voxel_size, bounding_box, isovalue, closed, show_stats);
|
||||
module metaballs(spec, voxel_size, bounding_box, isovalue=1, closed=true, grow_bounds=true, auto_voxels=8000, convexity=6, cp="centroid", anchor="origin", spin=0, orient=UP, atype="hull", show_stats=false, show_box=false) {
|
||||
vnf = metaballs(spec, voxel_size, bounding_box, isovalue, closed, grow_bounds, auto_voxels, show_stats);
|
||||
vnf_polyhedron(vnf, convexity=convexity, cp=cp, anchor=anchor, spin=spin, orient=orient, atype=atype)
|
||||
children();
|
||||
if(show_box)
|
||||
#translate(bounding_box[0]) cube(bounding_box[1]-bounding_box[0]);
|
||||
}
|
||||
|
||||
function metaballs(spec, voxel_size, bounding_box, isovalue=1, closed=true, show_stats=false) =
|
||||
function metaballs(spec, voxel_size, bounding_box, isovalue=1, closed=true, grow_bounds=true, auto_voxels=8000, show_stats=false) =
|
||||
assert(all_defined([spec, isovalue, bounding_box, voxel_size]), "\nThe parameters spec, isovalue, bounding_box, and voxel_size must all be defined.")
|
||||
assert(voxel_size=="auto" || (is_finite(voxel_size) && voxel_size>0) || (is_vector(voxel_size) && all_positive(voxel_size)), "\nvoxel_size must be a positive number, a 3-vector of positive values, or \"auto\".")
|
||||
assert(is_finite(isovalue) || (is_list(isovalue) && len(isovalue)==2 && is_num(isovalue[0]) && is_num(isovalue[1])), "\nIsovalue must be a number or a range; a number is the same as [number,INF].")
|
||||
assert(len(spec)%2==0, "\nThe spec parameter must be an even-length list of alternating transforms and functions")
|
||||
let(
|
||||
isoval = is_list(isovalue) ? isovalue : [isovalue, INF],
|
||||
funclist = _mb_unwind_list(spec),
|
||||
nballs = len(funclist)/2,
|
||||
dummycheck = [
|
||||
@@ -1756,28 +1783,31 @@ function metaballs(spec, voxel_size, bounding_box, isovalue=1, closed=true, show
|
||||
transpose(select(matrix_inverse(funclist[j]), 0,2))
|
||||
],
|
||||
|
||||
// new bounding box centered around original, forced to integer multiples of voxel size
|
||||
halfvox = 0.5*voxel_size,
|
||||
bbcenter = mean(bounding_box),
|
||||
bbnums = v_ceil((bounding_box[1]-bounding_box[0]) / voxel_size),
|
||||
newbbox = [bbcenter - halfvox*bbnums, bbcenter + halfvox*bbnums],
|
||||
// new voxel or bounding box centered around original, to fit whole voxels
|
||||
autovoxsize = voxel_size == "auto" ? _getautovoxsize(bounding_box, auto_voxels) : voxel_size,
|
||||
voxsize = _getvoxsize(autovoxsize, bounding_box, grow_bounds),
|
||||
bbox0 = is_num(bounding_box)
|
||||
? let(hb=0.5*bounding_box) _getbbox(autovoxsize, [[-hb,-hb,-hb],[hb,hb,hb]])
|
||||
: bounding_box,
|
||||
newbbox = _getbbox(autovoxsize, bbox0, grow_bounds),
|
||||
|
||||
// set up field array
|
||||
bot = newbbox[0],
|
||||
top = newbbox[1],
|
||||
halfvox = 0.5*voxsize,
|
||||
// accumulate metaball contributions using matrices rather than sums
|
||||
xset = [bot.x:voxel_size:top.x+halfvox],
|
||||
yset = list([bot.y:voxel_size:top.y+halfvox]),
|
||||
zset = list([bot.z:voxel_size:top.z+halfvox]),
|
||||
xset = [bot.x:voxsize.x:top.x+halfvox.x],
|
||||
yset = list([bot.y:voxsize.y:top.y+halfvox.y]),
|
||||
zset = list([bot.z:voxsize.z:top.z+halfvox.z]),
|
||||
allpts = [for(x=xset, y=yset, z=zset) [x,y,z,1]],
|
||||
trans_pts = [for(i=[0:nballs-1]) allpts*transmatrix[i]],
|
||||
allvals = [for(i=[0:nballs-1]) [for(pt=trans_pts[i]) funclist[2*i+1](pt)]],
|
||||
//total = _sum(allvals,allvals[0]*EPSILON),
|
||||
total = _sum(slice(allvals,1,-1), allvals[0]),
|
||||
fieldarray = list_to_matrix(list_to_matrix(total,len(zset)),len(yset))
|
||||
) isosurface(fieldarray, isovalue, voxel_size, closed=closed, show_stats=show_stats, _mb_origin=newbbox[0]);
|
||||
|
||||
) isosurface(fieldarray, isoval, voxsize, closed=closed, show_stats=show_stats, _mb_origin=newbbox[0]);
|
||||
|
||||
/// internal function: unwrap nested metaball specs in to a single list
|
||||
function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
let(
|
||||
dum1 = assert(is_list(list), "\nDid not find valid list of metaballs."),
|
||||
@@ -1806,12 +1836,11 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// SynTags: Geom,VNF
|
||||
// Topics: Isosurfaces, VNF Generators
|
||||
// Usage: As a module
|
||||
// isosurface(f, isovalue, voxel_size, bounding_box, [reverse=], [closed=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// isosurface(f, isovalue, voxel_size, bounding_box, [reverse=], [closed=], [grow_bounds=], [auto_voxels=], [show_stats=], ...) [ATTACHMENTS];
|
||||
// Usage: As a function
|
||||
// vnf = isosurface(f, isovalue, voxel_size, bounding_box, [reverse=], [closed=], [show_stats=]);
|
||||
// vnf = isosurface(f, isovalue, voxel_size, bounding_box, [reverse=], [closed=], [grow_bounds=], [auto_voxels=], [show_stats=]);
|
||||
// Description:
|
||||
// Computes a [VNF structure](vnf.scad) of a 3D isosurface within a bounded box at a single
|
||||
// isovalue or range of isovalues.
|
||||
// Computes a [VNF structure](vnf.scad) of an object bounded by an isosurface or a range between two isosurfaces, within a specified bounding box.
|
||||
// The isosurface of a function $f(x,y,z)$ is the set of points where $f(x,y,z)=c$ for some
|
||||
// constant isovalue $c$.
|
||||
// To provide a function, you supply a [function literal](https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/User-Defined_Functions_and_Modules#Function_literals)
|
||||
@@ -1821,50 +1850,67 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// case the isosurface is the set of points equal to the isovalue as interpolated from the array.
|
||||
// The array indices are in the order `[x][y][z]`.
|
||||
// .
|
||||
// The VNF that is computed has the isosurface as its bounding surface, with all the points where
|
||||
// $f(x,y,z)>c$ on the interior side of the surface.
|
||||
// When the isovalue is a range, `[c1, c2]`, then the resulting VNF has two bounding surfaces
|
||||
// corresponding to `c1` and `c2`, and the interior of the object are the points with intermediate
|
||||
// isovalues; this generally produces a shell object that has an inside and outside surface. The
|
||||
// range can start at `-INF` or end at `INF`. A single isovalue `c` is equivalent to `[c,INF]`.
|
||||
// The specified isovalue must be a range $[c_1,c_2]$. The returned object is the set of points $p$ that
|
||||
// satisfy $c_1 \leq f(p) \leq c_2$. If $f$ has values larger than $c_2$ and values smaller than $c_1$,
|
||||
// then the result is a VNF with two bounding surfaces corresponding to the isosurfaces at $c_1$ and
|
||||
// $c_2$. This is a shell object having two surfaces with a gap between them: the front faces of each
|
||||
// surface face away from each other, and the backs face each other across the gap. If $f(p)<c_2$
|
||||
// everywhere (which is true when $c_2 = \infty$), then no isosurface exists for $c_2$, so the object
|
||||
// has only one bounding surface — the one defined by $c_1$. This can result in a bounded object
|
||||
// like a sphere, or it can result an an unbounded object such as all the points outside of a sphere out
|
||||
// to infinity. A similar situation arises if $f(p)>c_1$ everywhere (which is true when
|
||||
// $c_1 = -\infty$). Setting isovalue to `[-INF,c2]` or `[c1,INF]` always produces an object with a
|
||||
// single bounding isosurface. To obtain a bounded object, think about whether the function values
|
||||
// inside your object are smaller or larger than your isosurface value. If the values inside are
|
||||
// smaller, you produce a bounded object using `[-INF,c]`. If the values inside are larger, you get a
|
||||
// bounded object using `[c,INF]`.
|
||||
// .
|
||||
// The isosurface is evaluated over a bounding box defined by its minimum and maximum corners,
|
||||
// `[[xmin,ymin,zmin],[xmax,ymax,zmax]]`. This bounding box is divided into voxels of the
|
||||
// specified `voxel_size`. Smaller voxels produce a finer, smoother result at the expense of
|
||||
// execution time. If the voxel size doesn't exactly divide your specified bounding box, then
|
||||
// the bounding box is enlarged to contain whole voxels, and centered on your requested box. If
|
||||
// execution time. By default, if the voxel size doesn't exactly divide your specified bounding box, then
|
||||
// the bounding box is enlarged to contain whole voxels, and centered on your requested box (or, you can
|
||||
// set `grow_bounds=false` to force the voxels to adjust in size to fit instead). If
|
||||
// the bounding box clips the isosurface and `closed=true` (the default), a surface is added to create
|
||||
// a closed manifold object. Setting `closed=false` causes the VNF to end at the bounding box,
|
||||
// resulting in a non-manifold shape that exposes the inside of the object.
|
||||
// .
|
||||
// If your object is unbounded then when it intersects with the bounding box and `closed=true`, the
|
||||
// result may appear like a solid cube, because the clipping faces are all you can see and the bounding
|
||||
// surface is hidden inside. Setting `closed=false` removes the bounding box faces and exposes the
|
||||
// inside structure. If you want the bounded object, you can correct this problem by changing the
|
||||
// isovalue range: one of `[-INF,c2]` or `[c1,INF]` or `[c1,c2]` should do the job.
|
||||
// .
|
||||
// The `voxel_size` and `bounding_box` parameters affect the run time, which can be long.
|
||||
// A voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the
|
||||
// calculation and storage of 8,000,000 function values, and more processing and memory to generate
|
||||
// the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the
|
||||
// number of voxels below 10,000 for preview, and adjust the voxel size smaller for final
|
||||
// rendering. A bounding box that is larger than your isosurface wastes time computing function
|
||||
// values that are not needed. You can also set the parameter `show_stats=true` to get the bounds of the
|
||||
// voxels the surface intersects. With this information, you may be able to decrease run time, or keep
|
||||
// the same run time but increase the resolution.
|
||||
// requires only 8,000 function values and a modest computation time. A good rule is to keep the number
|
||||
// of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. Setting
|
||||
// `voxel_size="auto"` sets a size such that approximately 8,000 voxels fit within your bounding box,
|
||||
// which should be reasonable for initial preview. Because a bounding box that is too large wastes time
|
||||
// computing function values that are not needed, you can also set the parameter `show_stats=true` to
|
||||
// get the actual bounds of the voxels intersected by the surface. With this information, you may be
|
||||
// able to decrease run time, or keep the same run time but increase the resolution.
|
||||
// .
|
||||
// The point list in the VNF structure contains many duplicated points. This is not a
|
||||
// problem for rendering the shape, but if you want to eliminate these, you can pass
|
||||
// the structure to {{vnf_merge_points()}}. Additionally, flat surfaces (often
|
||||
// resulting from clipping by the bounding box) are triangulated at the voxel size
|
||||
// resolution, and these can be unified into a single face by passing the vnf
|
||||
// structure to {{vnf_unify_faces()}}. These steps can be computationally expensive
|
||||
// The point list in the VNF structure contains many duplicated points. This is not a problem for
|
||||
// rendering the shape, but if you want to eliminate these, you can pass the structure to
|
||||
// {{vnf_merge_points()}}. Additionally, flat surfaces (often resulting from clipping by the bounding
|
||||
// box) are triangulated at the voxel size resolution, and these can be unified into a single face by
|
||||
// passing the vnf structure to {{vnf_unify_faces()}}. These steps can be computationally expensive
|
||||
// and are not normally necessary.
|
||||
// Arguments:
|
||||
// f = The isosurface function or array.
|
||||
// isovalue = a scalar giving the isovalue parameter or a 2-vector giving an isovalue range.
|
||||
// voxel_size = scalar size of the voxel cube that is used to sample the volume.
|
||||
// bounding_box = When `f` is a function, a pair of 3D points `[[xmin,ymin,zmin], [xmax,ymax,zmax]]`, specifying the minimum and maximum corner coordinates of the volume of space in which to perform computations. The actual bounding box is enlarged if necessary to fit whole the voxels, and centered around your requested box. When `f` is an array of values, `bounding_box` is already implied by the array size combined with `voxel_size`, in which case this implied bounding box is centered around the origin.
|
||||
// isovalue = A 2-vector giving an isovalue range. For an unbounded range, use `[-INF, max_isovalue]` or `[min_isovalue, INF]`.
|
||||
// voxel_size = size of the voxel that is used to sample the bounding box volume. This can be "auto", a scalar size for a cubical voxel, or a 3-vector if you want non-cubical voxels. For "auto", the voxel size is set so that approximately `auto_voxels` (default 8000) quantity of voxels fit inside the bounding box. If you set `grow_bounds=false`, then bounding box is held fixed in size, and the voxel size is adjusted as needed so that whole voxels fit inside the bounding box.
|
||||
// bounding_box = A designation of volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points `[[xmin,ymin,zmin] [xmax,ymax,zmax]]`, specifying the minimum and maximum box corner coordinates. With the default `grow_bounds=true`, the actual bounding box is enlarged if necessary to fit whole voxels, and centered around your requested box. When `f` is an array of values, `bounding_box` is already implied by the array size combined with `voxel_size`, in which case this implied bounding box is centered around the origin.
|
||||
// ---
|
||||
// closed = When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face and instead produce a non-manfold VNF that has holes. Default: true
|
||||
// reverse = When true, reverses the orientation of the VNF faces. Default: false
|
||||
// grow_bounds = When true, enlarges `bounding_box` as needed to fit whole voxels of `voxel_size`, and centers the new bounding box over the requested box. When false, shrinks voxels as needed to fit whole voxels inside the requested bounding box. Default: true
|
||||
// show_stats = If true, display statistics in the console window about the isosurface: number of voxels that the surface passes through, number of triangles, bounding box of the voxels, and voxel-rounded bounding box of the surface, which may help you reduce your bounding box to improve speed. Enabling this parameter has a slight speed penalty. Default: false
|
||||
// show_box = (Module only) display the requested bounding box as transparent. This box may appear slightly inside the bounds of the figure if the actual bounding box had to be expanded to accommodate whole voxels. Default: false
|
||||
// auto_voxels = Approximate quanity of voxels to have in the bounding box when `voxel_size="auto"`. Useful for fast preview of a reasonable number of voxels. Use with `show_stats=true` to see the corresponding voxel size. Default: 8000
|
||||
// convexity = (Module only) Maximum number of times a line could intersect a wall of the shape. Affects preview only. Default: 6
|
||||
// cp = (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
|
||||
// anchor = (Module only) Translate so anchor point is at origin (0,0,0). See [anchor](attachments.scad#subsection-anchor). Default: `"origin"`
|
||||
@@ -1876,40 +1922,54 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// "intersect" = Anchors to the surface of the shape.
|
||||
// Named Anchors:
|
||||
// "origin" = Anchor at the origin, oriented UP.
|
||||
// Example(3D,ThrownTogether,NoAxes): A gyroid is an isosurface defined by all the zero values of a 3D periodic function. To illustrate what the surface looks like, `closed=false` has been set to expose both sides of the surface. The surface is periodic and tileable along all three axis directions. This a non-manifold surface as displayed, not useful for 3D modeling. This example also demonstrates using an additional parameter in the field function beyond just the [x,y,z] input; in this case controls the wavelength of the gyroid.
|
||||
// Example(3D,VPD=85,VPT=[0,0,2],VPR=[55,0,30]): These first three examples demonstrate the effect of isovalue range for the simplest of all surfaces: a sphere where $r=\sqrt{x^2+y^2+z^2}$, or `r = norm([x,y,z])` in OpenSCAD, in which the isosurface at `r` exists at every `[x,y,z]` point where the expression equals `r`. We use the isovalue range `[-INF,10]` here to make a sphere of radius 10, with a bounding box that cuts off half the sphere. The isovalue range could also be `[0,10]` because the minimum value of the expression is zero.
|
||||
// isovalue = [-INF,10];
|
||||
// bbox = [[-11,-11,-11], [0,11,11]];
|
||||
// isosurface(function (xyz) norm(xyz),
|
||||
// isovalue, voxel_size = 1,
|
||||
// bounding_box = bbox);
|
||||
// Example(3D,VPD=85,VPT=[0,0,2],VPR=[55,0,30]): In this second example, if we the isovalue to a range between 8 and 10, we get a shell with interior radius 8 and exterior radius 10.
|
||||
// isovalue = [8,10];
|
||||
// bbox = [[-11,-11,-11], [0,11,11]];
|
||||
// isosurface(function (xyz) norm(xyz),
|
||||
// isovalue, voxel_size = 1,
|
||||
// bounding_box = bbox);
|
||||
// Example(3D,VPD=85,VPT=[0,0,2],VPR=[55,0,30]): In this third example, we change the bounds so that the sphere radius is still 10 but the upper bound is infinity. Because the sphere expression `norm(xyz)` has larger values growing to infinity with distance from the origin, the resulting object appears as the bounding box with the minimum isovalue (the sphere) cut out of it.
|
||||
// isovalue = [10,INF];
|
||||
// bbox = [[-11,-11,-11], [0,11,11]];
|
||||
// isosurface(function (xyz) norm(xyz),
|
||||
// isovalue, voxel_size = 1,
|
||||
// bounding_box = bbox);
|
||||
// Example(3D,ThrownTogether,NoAxes): A gyroid is an isosurface defined by all the zero values of a 3D periodic function. To illustrate what the surface looks like, `closed=false` has been set to expose both sides of the surface. The surface is periodic and tileable along all three axis directions. This is a non-manifold surface as displayed, not useful for 3D modeling. This example also demonstrates using an additional parameter in the field function beyond just the `[x,y,z]` input; in this case to control the wavelength of the gyroid.
|
||||
// function gyroid(xyz, wavelength) = let(
|
||||
// p = 360/wavelength,
|
||||
// px = p*xyz.x, py = p*xyz.y, pz = p*xyz.z
|
||||
// ) sin(px)*cos(py) + sin(py)*cos(pz) + sin(pz)*cos(px);
|
||||
// isovalue = 0;
|
||||
// p = 360/wavelength * xyz
|
||||
// ) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
|
||||
// isovalue = [0,INF];
|
||||
// bbox = [[-100,-100,-100], [100,100,100]];
|
||||
// isosurface(function (xyz) gyroid(xyz, wavelength=200),
|
||||
// isovalue, voxel_size=5, bounding_box=bbox,
|
||||
// closed=false);
|
||||
// Example(3D,NoAxes): If we remove the `closed` parameter or set it to true, the isosurface algorithm encloses the entire half-space bounded by the "inner" gyroid surface, leaving only the "outer" surface exposed. This is a manifold shape but not what we want if trying to model a gyroid.
|
||||
// function gyroid(xyz, wavelength) = let(
|
||||
// p = 360/wavelength,
|
||||
// px = p*xyz.x, py = p*xyz.y, pz = p*xyz.z
|
||||
// ) sin(px)*cos(py) + sin(py)*cos(pz) + sin(pz)*cos(px);
|
||||
// isovalue = 0;
|
||||
// p = 360/wavelength * xyz
|
||||
// ) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
|
||||
// isovalue = [0,INF];
|
||||
// bbox = [[-100,-100,-100], [100,100,100]];
|
||||
// isosurface(function (xyz) gyroid(xyz, wavelength=200),
|
||||
// isovalue, voxel_size=5, bounding_box=bbox);
|
||||
// Example(3D,ThrownTogether,NoAxes): To make the gyroid a double-sided surface, we need to specify a small range around zero for `isovalue`. Now we have a double-sided surface although with `closed=false` the edges are not closed where the surface is clipped by the bounding box.
|
||||
// function gyroid(xyz, wavelength) = let(
|
||||
// p = 360/wavelength,
|
||||
// px = p*xyz.x, py = p*xyz.y, pz = p*xyz.z
|
||||
// ) sin(px)*cos(py) + sin(py)*cos(pz) + sin(pz)*cos(px);
|
||||
// p = 360/wavelength * xyz
|
||||
// ) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
|
||||
// isovalue = [-0.3, 0.3];
|
||||
// bbox = [[-100,-100,-100], [100,100,100]];
|
||||
// isosurface(function (xyz) gyroid(xyz, wavelength=200),
|
||||
// isovalue, voxel_size=5, bounding_box=bbox,
|
||||
// closed = false);
|
||||
// Example(3D,ThrownTogether,NoAxes): To make the gyroid a valid manifold 3D object, we remove the `closed` parameter (same as setting `closed=true`), which closes the edges where the surface is clipped by the bounding box. The resulting object can be tiled, the VNF returned by the functional version can be wrapped around an axis using {{vnf_bend()}}, and other operations.
|
||||
// Example(3D,ThrownTogether,NoAxes): To make the gyroid a valid manifold 3D object, we remove the `closed` parameter (same as setting `closed=true`), which closes the edges where the surface is clipped by the bounding box.
|
||||
// function gyroid(xyz, wavelength) = let(
|
||||
// p = 360/wavelength,
|
||||
// px = p*xyz.x, py = p*xyz.y, pz = p*xyz.z
|
||||
// ) sin(px)*cos(py) + sin(py)*cos(pz) + sin(pz)*cos(px);
|
||||
// p = 360/wavelength * xyz
|
||||
// ) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
|
||||
// isovalue = [-0.3, 0.3];
|
||||
// bbox = [[-100,-100,-100], [100,100,100]];
|
||||
// isosurface(function (xyz) gyroid(xyz, wavelength=200),
|
||||
@@ -1934,17 +1994,26 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// isovalue, voxel_size=4, bounding_box=bbox);
|
||||
// Example(3D,NoAxes): Example of a bounded isosurface.
|
||||
// isosurface(
|
||||
// function (x,y,z)
|
||||
// let(a=xyz_to_spherical(x,y,z),
|
||||
// function (xyz)
|
||||
// let(a=xyz_to_spherical(xyz),
|
||||
// r=a[0],
|
||||
// phi=a[1],
|
||||
// theta=a[2]
|
||||
// ) 1/(r*(3+cos(5*phi)+cos(4*theta))),
|
||||
// isovalue = 0.1,
|
||||
// isovalue = [0.1,INF],
|
||||
// voxel_size = 0.25,
|
||||
// bounding_box = [[-8,-7,-8],[6,7,8]], show_stats=true
|
||||
// bounding_box = [[-8,-7,-8],[6,7,8]]
|
||||
// );
|
||||
// Example(3D): Using an array for the `f` argument instead of a function literal.
|
||||
// Example(3D,NoAxes): For shapes that occupy a cubical bounding box centered on the origin, you can simply specify a scalar for the size of the box.
|
||||
// isosurface(
|
||||
// function (p) (p.x*p.y*p.z^3 + 19*p.x^2*p.z^2)/norm(p)^2 + norm(p)^2,
|
||||
// isovalue=[-INF,35], bounding_box=12, voxel_size=0.25);
|
||||
// Example(3D,Med,NoAxes,VPD=165,VPR=[72,0,290],VPT=[0,0,0]): An object that could be a sort of support pillar. Here we set `show_box=true` to reveal that the bounding box is slightly bigger than it needs to be. The argument `show_stats=true` also outputs the voxel bounding box size as a suggestion of what it should be.
|
||||
// isosurface(
|
||||
// function (p) (p.x*p.y*p.z^3 - 3*p.x^2*p.z^2)/norm(p)^2 + norm(p)^2,
|
||||
// isovalue=[-INF,35], bounding_box=[[-32,-32,-14],[32,32,14]],
|
||||
// voxel_size = 0.8, show_box=true);
|
||||
// Example(3D): Using an array for the `f` argument instead of a function literal. Each row of the array represents an X index for a YZ plane with the array Z indices changing fastest in each plane. The final object may need rotation to get the orientation you want. You don't pass the `bounding_box` argument here; it is implied by the array size and voxel size, and centered on the origin.
|
||||
// field = [
|
||||
// repeat(0,[6,6]),
|
||||
// [ [0,1,2,2,1,0],
|
||||
@@ -1971,42 +2040,76 @@ function _mb_unwind_list(list, parent_trans=[IDENT]) =
|
||||
// repeat(0,[6,6])
|
||||
// ];
|
||||
// rotate([0,-90,180])
|
||||
// isosurface(field, isovalue=0.5,
|
||||
// isosurface(field, isovalue=[0.5,INF],
|
||||
// voxel_size=10);
|
||||
|
||||
module isosurface(f, isovalue, voxel_size, bounding_box, reverse=false, closed=true, convexity=6, cp="centroid", anchor="origin", spin=0, orient=UP, atype="hull", show_stats=false, show_box=false, _mb_origin=undef) {
|
||||
vnf = isosurface(f, isovalue, voxel_size, bounding_box, reverse, closed, show_stats, _mb_origin);
|
||||
module isosurface(f, isovalue, voxel_size, bounding_box, reverse=false, closed=true, grow_bounds=true, auto_voxels=8000, convexity=6, cp="centroid", anchor="origin", spin=0, orient=UP, atype="hull", show_stats=false, show_box=false, _mb_origin=undef) {
|
||||
vnf = isosurface(f, isovalue, voxel_size, bounding_box, reverse, closed, grow_bounds, auto_voxels, show_stats, _mb_origin);
|
||||
vnf_polyhedron(vnf, convexity=convexity, cp=cp, anchor=anchor, spin=spin, orient=orient, atype=atype)
|
||||
children();
|
||||
if(show_box)
|
||||
#translate(bounding_box[0]) cube(bounding_box[1]-bounding_box[0]);
|
||||
%translate(bounding_box[0]) cube(bounding_box[1]-bounding_box[0]);
|
||||
}
|
||||
|
||||
function isosurface(f, isovalue, voxel_size, bounding_box, reverse=false, closed=true, show_stats=false, _mb_origin=undef) =
|
||||
function isosurface(f, isovalue, voxel_size, bounding_box, reverse=false, closed=true, grow_bounds=true, auto_voxels=8000, show_stats=false, _mb_origin=undef) =
|
||||
assert(all_defined([f, isovalue, voxel_size]), "\nThe parameters f, isovalue, and voxel_size must all be defined.")
|
||||
assert(voxel_size=="auto" || (is_finite(voxel_size) && voxel_size>0) || (is_vector(voxel_size) && all_positive(voxel_size)), "\nvoxel_size must be a positive number, a 3-vector of positive values, or \"auto\".")
|
||||
assert(is_list(isovalue) && len(isovalue)==2 && is_num(isovalue[0]) && is_num(isovalue[1]), "\nIsovalue must be a range; use [minvalue,INF] or [-INF,maxvalue] for an unbounded range.")
|
||||
assert((is_function(f) && is_def(bounding_box)) || (is_list(f) && is_undef(bounding_box)),
|
||||
"\nbounding_box must be passed if f is a function, and cannot be passed if f is an array.")
|
||||
|
||||
let(
|
||||
isovalmin = is_list(isovalue) ? isovalue[0] : isovalue,
|
||||
isovalmax = is_list(isovalue) ? isovalue[1] : INF,
|
||||
dum1 = assert(isovalmin < isovalmax, str("\nBad isovalue range (", isovalmin, ", >= ", isovalmax, "), should be expressed as [min_value, max_value].")),
|
||||
hv = 0.5*voxel_size,
|
||||
bbox = is_function(f)
|
||||
? let( // new bounding box quantized for voxel_size, centered around original box
|
||||
bbcenter = mean(bounding_box),
|
||||
bbn = v_ceil((bounding_box[1]-bounding_box[0]) / voxel_size)
|
||||
) [bbcenter - hv*bbn, bbcenter + hv*bbn]
|
||||
dumiso1 = assert(isovalmin < isovalmax, str("\nBad isovalue range (", isovalmin, ", >= ", isovalmax, "), should be expressed as [min_value, max_value].")),
|
||||
dumiso2 = assert(isovalmin != -INF || isovalmin != INF, "\nIsovalue range must be finite on one end."),
|
||||
autovoxsize = voxel_size == "auto" ? _getautovoxsize(bounding_box, auto_voxels) : voxel_size,
|
||||
voxsize = _getvoxsize(autovoxsize, bounding_box, grow_bounds),
|
||||
bbox0 = is_num(bounding_box)
|
||||
? let(hb=0.5*bounding_box) _getbbox(autovoxsize, [[-hb,-hb,-hb],[hb,hb,hb]])
|
||||
: bounding_box,
|
||||
bbox = is_function(f) ? _getbbox(autovoxsize, bbox0, grow_bounds)
|
||||
: let( // new bounding box, either centered on origin or using metaball origin
|
||||
hv = 0.5*voxsize,
|
||||
dims = list_shape(f) - [1,1,1]
|
||||
) is_def(_mb_origin)
|
||||
? [_mb_origin, _mb_origin+voxel_size*dims] // metaball bounding box
|
||||
: [-hv*dims, hv*dims], // centered bounding box
|
||||
cubes = _isosurface_cubes(voxel_size, bbox,
|
||||
? [_mb_origin, _mb_origin+v_mul(voxsize, dims)] // metaball bounding box
|
||||
: let(corner=v_mul(hv,dims)) [-corner, corner], // centered bounding box
|
||||
cubes = _isosurface_cubes(voxsize, bbox,
|
||||
fieldarray=is_function(f)?undef:f, fieldfunc=is_function(f)?f:undef,
|
||||
isovalmin=isovalmin, isovalmax=isovalmax, closed=closed),
|
||||
tritablemin = reverse ? _MCTriangleTable_reverse : _MCTriangleTable,
|
||||
tritablemax = reverse ? _MCTriangleTable : _MCTriangleTable_reverse,
|
||||
trianglepoints = _isosurface_triangles(cubes, voxel_size, isovalmin, isovalmax, tritablemin, tritablemax),
|
||||
trianglepoints = _isosurface_triangles(cubes, voxsize, isovalmin, isovalmax, tritablemin, tritablemax),
|
||||
faces = [ for(i=[0:3:len(trianglepoints)-1]) [i,i+1,i+2] ],
|
||||
dum2 = show_stats ? _showstats_isosurface(voxel_size, bbox, isovalmin, cubes, trianglepoints, faces) : 0
|
||||
dum2 = show_stats ? _showstats_isosurface(voxsize, bbox, isovalue, cubes, trianglepoints, faces) : 0
|
||||
) [trianglepoints, faces];
|
||||
|
||||
// internal function: get "auto" voxel size given a desired number of voxels in a bounding box
|
||||
function _getautovoxsize(bbox, numvoxels) =
|
||||
let(
|
||||
bbsiz = bbox[1]-bbox[0],
|
||||
bbvol = bbsiz[0]*bbsiz[1]*bbsiz[2],
|
||||
voxvol = bbvol/numvoxels
|
||||
) voxvol^(1/3);
|
||||
|
||||
// internal function: get voxel size, adjusted if necessary to fit bounding box
|
||||
function _getvoxsize(voxel_size, bounding_box, grow_bounds) =
|
||||
let(voxsize0 = is_num(voxel_size) ? [voxel_size, voxel_size, voxel_size] : voxel_size)
|
||||
grow_bounds ? voxsize0 // if grow_bounds==true, we don't adjust voxel size
|
||||
: let(
|
||||
reqboxsize = bounding_box[1] - bounding_box[0],
|
||||
bbnums = v_ceil(v_div(bounding_box[1]-bounding_box[0], voxsize)),
|
||||
newboxsize = v_mul(bbnums, voxsize0)
|
||||
) v_mul(voxsize0, v_div(reqboxsize, newboxsize));
|
||||
|
||||
/// internal function: get bounding box, adjusted in size and centered on requested box
|
||||
function _getbbox(voxel_size, bounding_box, grow_bounds) =
|
||||
let(voxsize0 = is_num(voxel_size) ? [voxel_size, voxel_size, voxel_size] : voxel_size)
|
||||
grow_bounds ?
|
||||
let( // adjust bounding box
|
||||
bbcenter = mean(bounding_box),
|
||||
bbnums = v_ceil(v_div(bounding_box[1]-bounding_box[0], voxsize0)),
|
||||
halfbb = 0.5 * v_mul(voxsize0, bbnums)
|
||||
) [bbcenter - halfbb, bbcenter + halfbb]
|
||||
: bounding_box; // if grow_bounds==false, we don't adjust bounding box
|
||||
|
||||
Reference in New Issue
Block a user