dotSCAD/docs/lib3x-mz_theta.md

mz_theta

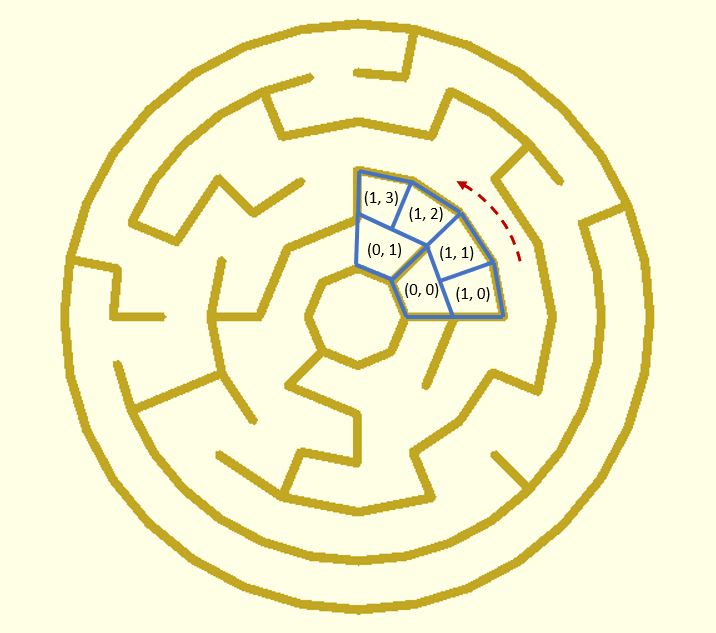
This function returns cell data of a theta maze. The data is a two-dimensional list with different row lengths. A cell has the data structure [ri, ci, type]. ri and ci are 0-based. ri means the ri-th ring and ci means the ci-th (counter-clockwise) cell of the ring.

The value of type is the wall type of the cell. It can be 0, 1, 2 or 3. Setting them to constants is convenient.

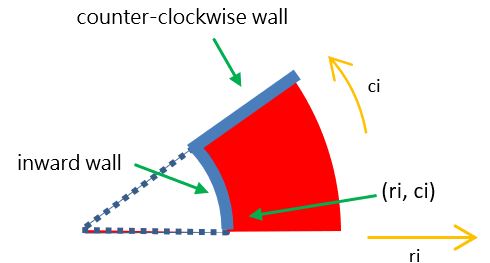
NO_WALL = 0;           // the cell has no wall
INWARD_WALL = 1;       // the cell has an inward wall
CCW_WALL = 2;          // the cell has a counter-clockwise wall
INWARD_CCW_WALL = 3;   // the cell has an inward wall and a clockwise wall

Since: 3.3

Parameters

• rings : The number of rings.
• beginning_number : The number of cells in the first row.
• start : The start point to travel the maze. Default to [0, 0].
• seed : The maze is traveling randomly. Use seed to initialize the pseudorandom number generator.

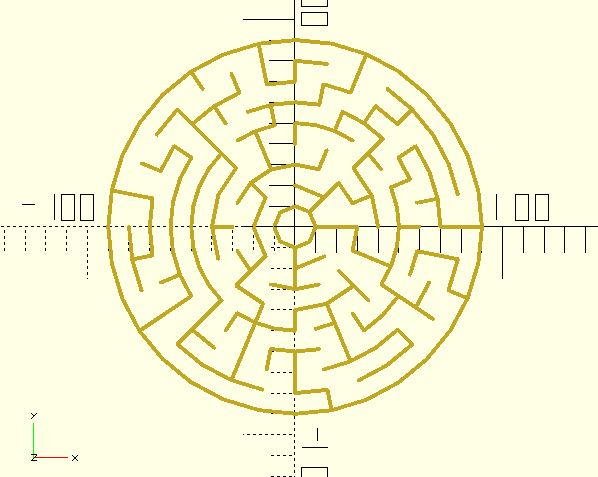
Examples

use <maze/mz_theta.scad>
use <polyline_join.scad>

rings = 8;
beginning_number = 8;
cell_width = 10;
wall_thickness = 2;

NO_WALL = 0;           
INWARD_WALL = 1;      
CCW_WALL = 2;         
INWARD_CCW_WALL = 3;   

function vt_from_angle(theta, r) = [r * cos(theta), r * sin(theta)];

maze = mz_theta(rings, beginning_number);

// draw cell walls
for(ring = maze, cell = ring) {		
	ri = cell[0];
	ci = cell[1];
	type = cell[2];
	thetaStep = 360 / len(maze[ri]);
	innerR = (ri + 1) * cell_width;
	outerR = (ri + 2) * cell_width;
	theta1 = thetaStep * ci;
	theta2 = thetaStep * (ci + 1);
	
	innerVt1 = vt_from_angle(theta1, innerR);
	innerVt2 = vt_from_angle(theta2, innerR);
	outerVt2 = vt_from_angle(theta2, outerR);
	
	if(type == INWARD_WALL || type == INWARD_CCW_WALL) {
		polyline_join([innerVt1, innerVt2])
			circle(wall_thickness / 2);
	}

	if(type == CCW_WALL || type == INWARD_CCW_WALL) {
		polyline_join([innerVt2, outerVt2])
			circle(wall_thickness / 2);
	}
}

// outmost walls
thetaStep = 360 / len(maze[rings - 1]);
r = cell_width * (rings + 1);
for(theta = [0:thetaStep:360 - thetaStep]) {
	vt1 = vt_from_angle(theta, r);
	vt2 = vt_from_angle(theta + thetaStep, r);
	polyline_join([vt1, vt2])
		circle(wall_thickness / 2);
}