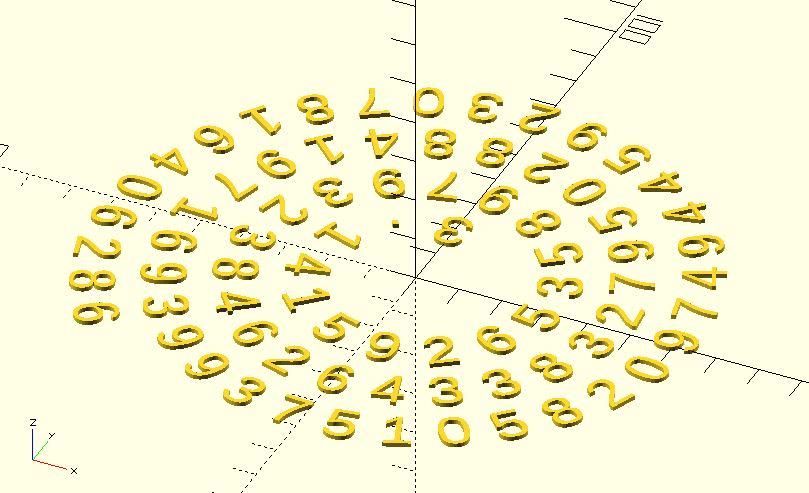mirror of
https://github.com/JustinSDK/dotSCAD.git
synced 2025-01-17 22:28:16 +01:00
2.4 KiB
2.4 KiB
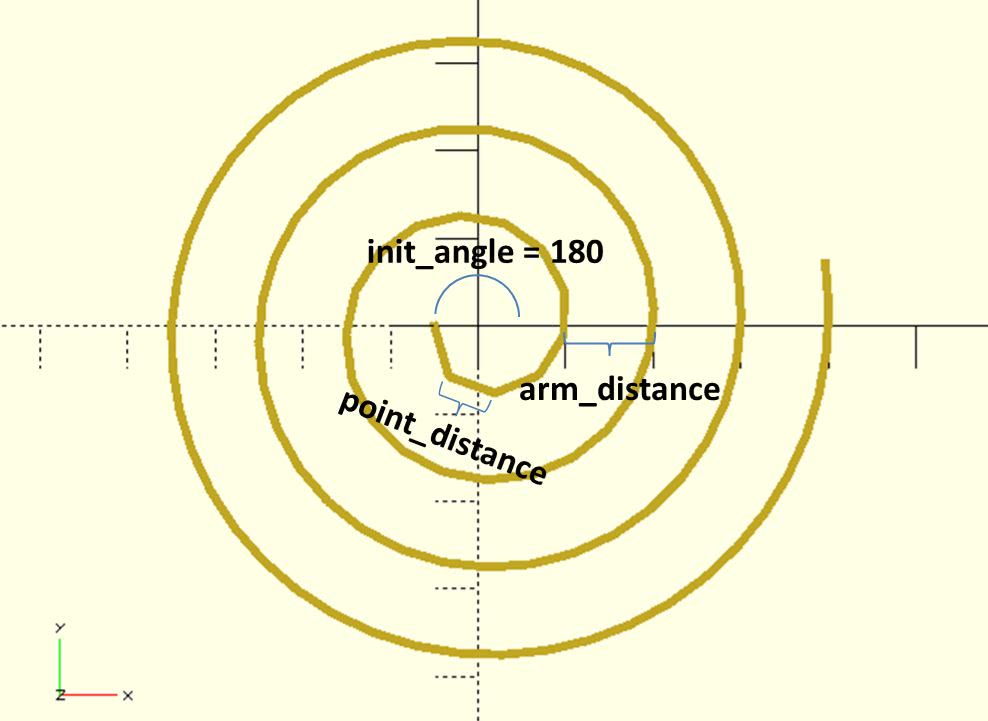
archimedean_spiral
Gets all points and angles on the path of an archimedean spiral. The distance between two points is almost constant.
It returns a vector of [[x, y], angle].
An init_angle less than 180 degrees is not recommended because the function uses an approximate approach. If you really want an init_angle less than 180 degrees, a larger arm_distance is required. To reduce the error value at the calculated distance between two points, you may try a smaller point_distance.
Parameters
arm_distance: If any ray from the origin intersects two successive turnings of the spiral, we'll have two points. Thearm_distanceis the distance between these two points.init_angle: In polar coordinates(r, θ)Archimedean spiral can be described by the equationr = bθwhereθis measured in radians. For being consistent with OpenSCAD, the function here use degrees. Theinit_angleis which angle the first point want to start.point_distance: Distance between two points on the path.num_of_points: How many points do you want?rt_dir:"CT_CLK"for counterclockwise."CLK"for clockwise. The default value is"CT_CLK".
Examples
include <line2d.scad>;
include <polyline2d.scad>;
include <archimedean_spiral.scad>;
points_angles = archimedean_spiral(
arm_distance = 10,
init_angle = 180,
point_distance = 5,
num_of_points = 100
);
points = [for(pa = points_angles) pa[0]];
polyline2d(points, width = 1);
include <archimedean_spiral.scad>;
points_angles = archimedean_spiral(
arm_distance = 10,
init_angle = 180,
point_distance = 5,
num_of_points = 100
);
for(pa = points_angles) {
translate(pa[0])
circle(2);
}
include <archimedean_spiral.scad>;
t = "3.141592653589793238462643383279502884197169399375105820974944592307816406286";
points = archimedean_spiral(
arm_distance = 15,
init_angle = 450,
point_distance = 12,
num_of_points = len(t)
);
for(i = [0: len(points) - 1]) {
translate(points[i][0])
rotate(points[i][1] + 90)
text(t[i], valign = "center", halign = "center");
}