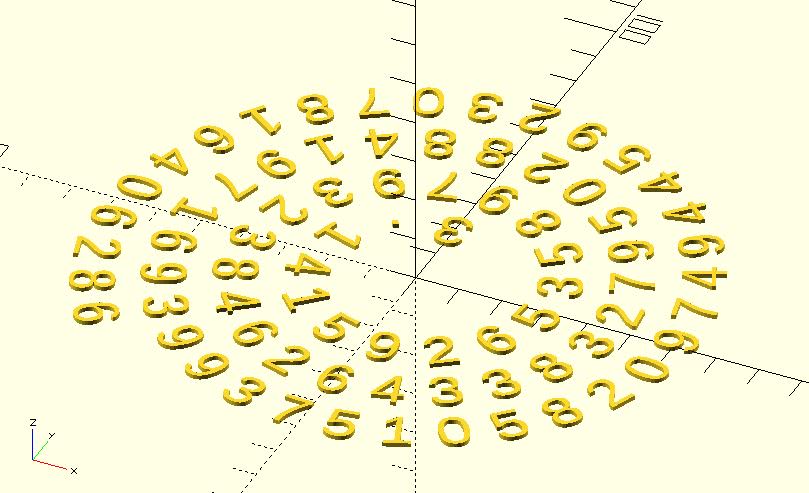dotSCAD/docs/lib3x-archimedean_spiral.md

archimedean_spiral

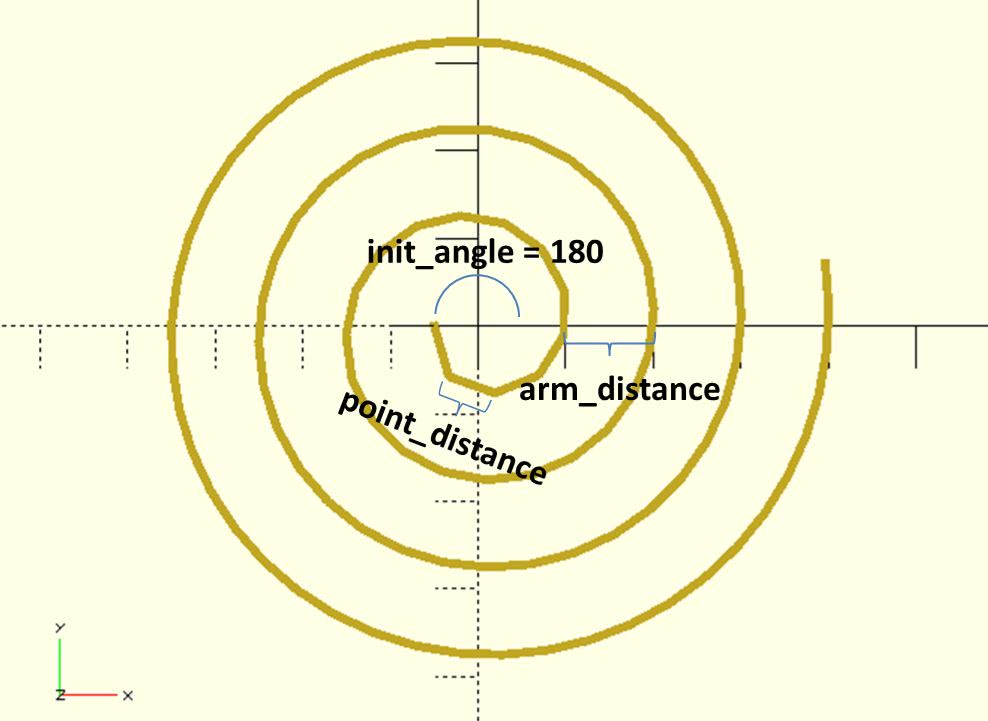
Gets all points and angles on the path of an archimedean spiral. The distance between two points is almost constant.

It returns a vector of [[x, y], angle].

An init_angle less than 180 degrees is not recommended because the function uses an approximate approach. If you really want an init_angle less than 180 degrees, a larger arm_distance is required. To reduce the error value at the calculated distance between two points, you may try a smaller point_distance.

Parameters

• arm_distance : If any ray from the origin intersects two successive turnings of the spiral, we'll have two points. The arm_distance is the distance between these two points.
• init_angle : In polar coordinates (r, θ) Archimedean spiral can be described by the equation r = bθ where θ is measured in radians. For being consistent with OpenSCAD, the function here use degrees. The init_angle is which angle the first point want to start.
• point_distance : Distance between two points on the path.
• num_of_points : How many points do you want?
• rt_dir : "CT_CLK" for counterclockwise. "CLK" for clockwise. The default value is "CT_CLK".

Examples

use <polyline2d.scad>
use <archimedean_spiral.scad>

points_angles = archimedean_spiral(
    arm_distance = 10,
    init_angle = 180,
    point_distance = 5,
    num_of_points = 100 
); 

points = [for(pa = points_angles) pa[0]];

polyline2d(points, width = 1);

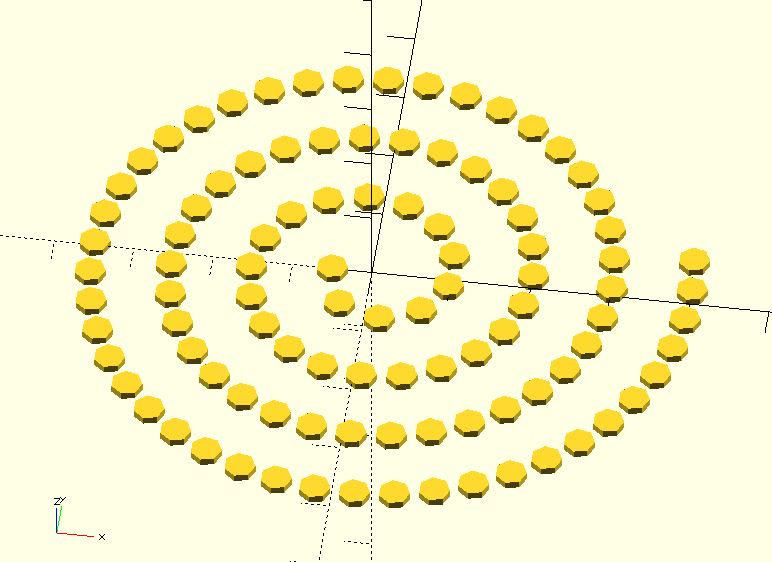
use <archimedean_spiral.scad>

points_angles = archimedean_spiral(
    arm_distance = 10,  
    init_angle = 180, 
    point_distance = 5,
    num_of_points = 100 
); 

for(pa = points_angles) {
    translate(pa[0]) 
        circle(2);
}

use <archimedean_spiral.scad>

t = "3.141592653589793238462643383279502884197169399375105820974944592307816406286";

points_angles = archimedean_spiral(
    arm_distance = 15,
    init_angle = 450, 
    point_distance = 12, 
    num_of_points = len(t) 
); 

for(i = [0: len(points_angles) - 1]) {
    translate(points_angles[i][0])          
    rotate(points_angles[i][1] + 90)  
        text(t[i], valign = "center", halign = "center");
}