dotSCAD/docs/lib3x-bspline_curve.md

bspline_curve

B-spline interpolation using de Boor's algorithm. This function returns points of the B-spline path.

Since: 2.1

Parameters

• t_step : The increment amount along the curve in the [0, 1] range.
• degree : The degree of B-spline. Must be less than or equal to len(points) - 1.
• points : A list of [x, y] or [x, y, z] control points.
• knots : The knot vector. It's a non-decreasing sequence with length len(points) + degree + 1. If not provided, a uniform knot vector is generated automatically.
• weights : The weights of control points. If not provided, the weight of each point is 1.

Examples

use <bspline_curve.scad>

points = [
	[-10, 0],
	[-5,  5],
	[ 5, -5],
	[ 10, 0]
];

color("red") for(p = points) {
	translate(p) 
		sphere(0.5);
}

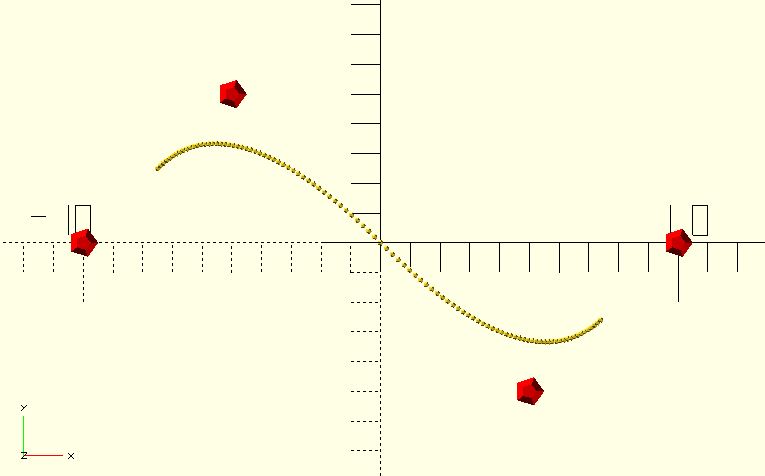
// knots: [0, 1, 2, 3, 4, 5, 6]
// weights: [1, 1, 1, 1]
for(p = bspline_curve(0.01, 2, points)) {
	translate(p) 
		sphere(0.1);
}

use <bspline_curve.scad>

points = [
	[-10, 0],
	[-5,  5],
	[ 5, -5],
	[ 10, 0]
];

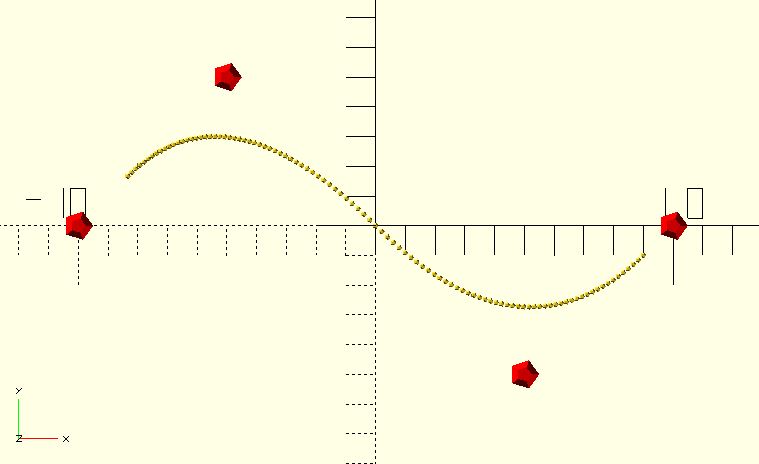
// a non-uniform B-spline curve
knots = [0, 1/8, 1/4, 1/2, 3/4, 4/5, 1];

color("red") 
for(p = points) {
	translate(p) 
		sphere(0.5);
}

for(p = bspline_curve(0.01, 2, points, knots)) {
	translate(p) 
		sphere(0.1);
}

use <bspline_curve.scad>
	
points = [
	[-10, 0],
	[-5,  5],
	[ 5, -5],
	[ 10, 0]
];

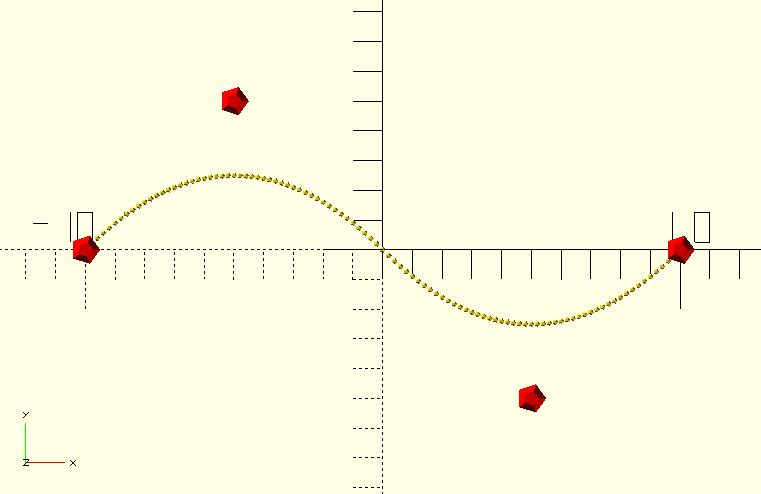
// For a clamped B-spline curve, the first `degree + 1` and the last `degree + 1` knots must be identical.
knots = [0, 0, 0, 1, 2, 2, 2];

color("red") 
for(p = points) {
	translate(p) 
		sphere(0.5);
}

for(p = bspline_curve(0.01, 2, points, knots)) {
	translate(p) 
		sphere(0.1);
}